Chapters

Number Line
A number line is defined as a representation of positive and negative real numbers. You’ve probably seen a number line before. The image below shows an example of a number line.

| Definition | Examples | |
| Negative Numbers | Below zero | -2, -6, -10 |
| Positive Numbers | Above zero | 5, 7, 10 |
| Origin | Middle point at zero | 0 |
| Arrows | Show that number line can continue |  , , 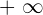 |
While a number line can include as many numbers as you want, it can be helpful to only include the range of numbers you’re interested in. A range is defined as all the values between two points. Take the following number lines as an example.

As you can see, number lines are pretty flexible. A half line uses number lines and is discussed a bit further.
Real Numbers
As stated in the previous section, a number line only takes real numbers into account. A real number can be:
| Definition | Examples | |
| Rational | Includes fraction or decimal | 3.44, 5.5,  |
| Irrational | Cannot be written as a fraction or decimal |  , , 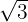 |
| Whole | Has no decimal | 2, 6, 98, 450 |
| Integer | Includes negative whole numbers | 1, -4, 6, -105 |
Inequalities
When we talk about using a half-line, we usually talk about it when using it to express inequalities. Inequalities are defined as the relative position, or size, of two numbers. Relative size is measured when we compare two values and determine which one is above, below or equal to the other.
| Sign | Explanation | Example |
| > | Greater than | 5 > 2 |
>=,  | Greater than or equal to | 3  3, 9 3, 9  1 1 |
| < | Less than | 1 < 3 |
<=,  | Less than or equal to | 2  2. 4 < 10 2. 4 < 10 |

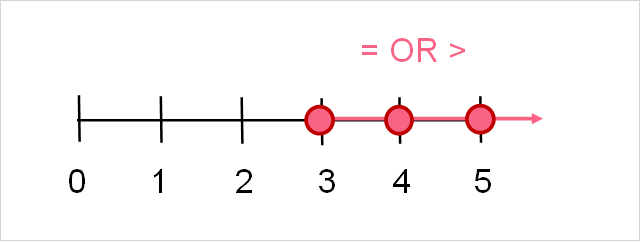
Greater Than
Let’s see how we can plot inequalities on a number line. Take the following example: you want to know which symbol can be used to fill in the following.


Greater Than or Equal To
This concept can be confusing, however it can be helpful to think of it as the combination of two different statements.

Less Than
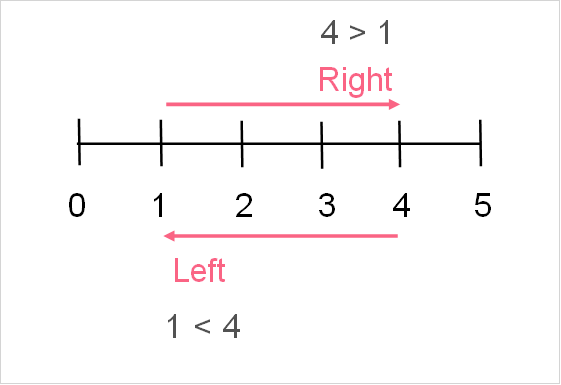
You want to buy something online - one product has a 1 star review, the other has a 5 star review. In this situation, we quickly determine that 1 is less than 5, made easier by the fact that a 1 star value is less than a 5 star value.
You can see this on the number line below, as 1 is to the left of 5. Any time a number is on the left of a value, it is less than that value.

Less Than or Equal To
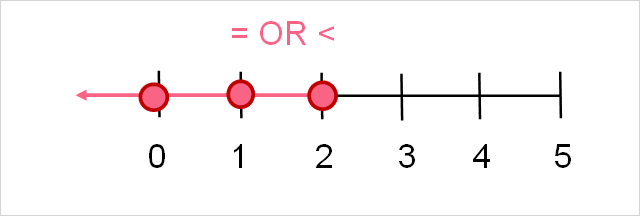
The concept of being less than or equal to is the same concept as  . It is the combination of two statements: a number that is less than OR equal to a value. Think of all possible numbers
. It is the combination of two statements: a number that is less than OR equal to a value. Think of all possible numbers  to 2. The number line below shows some examples.
to 2. The number line below shows some examples.
Rules
There are some rules you can use to help you determine whether a number is less than, equal to or greater than some value. The table below summarizes rules when dealing with a number line.
| Location on Number Line | Inequality | Written |
| To the left of a value | < | Less than |
| To the right of a value | > | Greater than |
| The same as a value | = | Equal to |
Another rule to keep in mind is that the same inequality can be written two ways.
Infinity
Infinity is an important concept in math. Infinity is not a real number and is endless. You can think of infinity as a company, where the only job is to count and keep the count going - no matter how long you count, you never reach infinity. It is written as the following:
\[
+ \infty, - \infty
\]
Union
When we write inequalities, we can write the interval in numbers instead of drawing it on a number line.
| Interval | Meaning | Interval Includes | Number line |
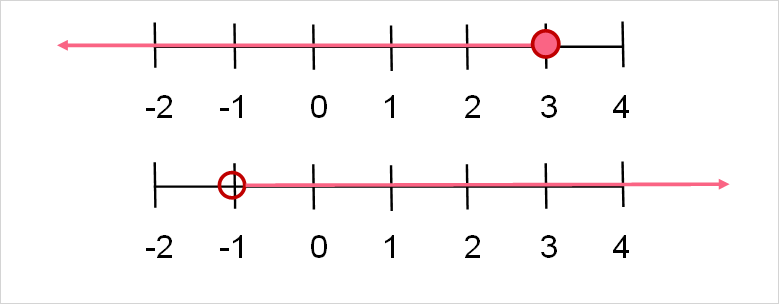
| (1,3) | () exclude the numbers of the interval | 2 | An empty circle |
| [1,3] | [] include the numbers of the interval | 1,2,3 | A filled in circle |
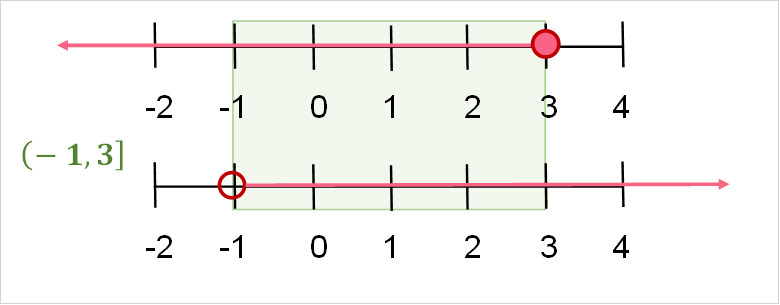
| (1,3] | A combination of the above two | 2,3 | A combination of the two above |
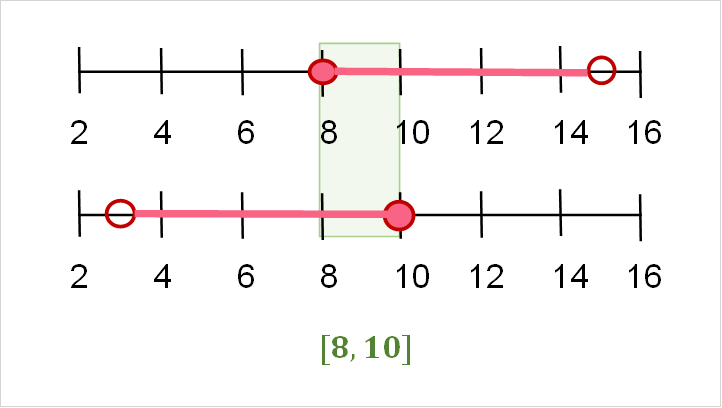
A union is a combination, or union, of two intervals. Take a look at the example below.

Intersection
An intersection is the interval where two intervals meet. In other words, when you take a union of two intervals, the intersection is the resulting interval. Here, we can understand what a half line is - a half line is lines which only move in one direction, and not both.
The two intervals in the union above are two examples of half-lines.
When we take the intersection, we are interested in the interval where both intervals meet.
Example 1
Take the following interval as an example: (5, + ). Is this a half-line or not?
). Is this a half-line or not?

Example 2
Find the intersection of the following union:
\[
(3, 10] \cap [8, 15)
\]
To solve this, we can plot the two intervals.