In this article, we will discuss what are powers or exponents, what are power formulas or rules of exponents, and how to use these formulas to simplify the expressions.

What is Power?
"The number of times a number or coefficient is multiplied by itself is known as the power or exponent of that number"
For example, if 2 is multiplied by itself 6 times, then we can write it mathematically as 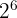 . It reflects that the number 2 is multiplied by itself 6 times. 6 is known as power, index, or exponent of the number 2. The number 2 is known as the base of the exponent.
. It reflects that the number 2 is multiplied by itself 6 times. 6 is known as power, index, or exponent of the number 2. The number 2 is known as the base of the exponent.
The procedure of using powers or exponents is also known as "raising to a power" because the exponent is also called power. The expression 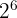 is pronounced as two raised to the power six. The most commonly used powers are 2 and 3. When an expression is raised to the power two, then we say that the expression is squared. On the other hand, if the expression is raised to power 3, then we say that the expression is cubed.
is pronounced as two raised to the power six. The most commonly used powers are 2 and 3. When an expression is raised to the power two, then we say that the expression is squared. On the other hand, if the expression is raised to power 3, then we say that the expression is cubed.
While writing numbers, we just simply write them as it is, instead of using the powers. For instance, we will use the number 81 instead of 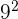 , however when we have to write the variables, then we must use exponents to write them in the simplified form. For example, we will not write "yyyy". Instead, we will write it as
, however when we have to write the variables, then we must use exponents to write them in the simplified form. For example, we will not write "yyyy". Instead, we will write it as  .
.
Now, we will discuss some of the power rules here which are also known as laws of exponents.
Power Rules
Zero Exponent Rule
This rule says that anything raised to the power zero is equal to 1. For example, if b is an expression, then  .
.
Power Rule
This rule basically describes what to do when powers are raised to the powers. For example, consider a number with the power that is further raised to another power. Mathematically, we can write this expression as:

In such a case, all you have to do is to multiply the exponents with each other. Mathematically, we can summarize this rule as:

Negative Exponent Rule
According to this rule, a negative exponent in the numerator becomes positive when it shifts to the denominator. Similarly, if we have a negative exponent in the denominator, then it becomes positive when we shift it to the numerator. Mathematically, we can write it as:

Product Rule
This rule says that when two exponents with the same bases are multiplied with each other, then we can simplify them by keeping the same base and adding up their exponents. Mathematically, we can write this rule as:
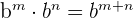
Quotient Rule
According to this rule, when two exponents with the same bases are divided, then we can simplify the exponents by keeping the bases the same and taking the difference of the exponents. This method resembles the process of reducing fractions. Mathematically, it can be written as:
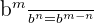
To avoid negative exponents, you can see where the higher power is located. If it is located in the numerator, then you can simply subtract the exponents and keep the base the same. However, when the higher power is in the denominator, then you can bring the exponent in the numerator to the denominator and take the difference of the highest and lowest power to avoid negative exponent.
Now, we will solve some examples using these power formulas or rules of exponents.
Example 1
Simplify  .
.
Solution
The exponents with similar bases will be added together.
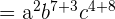
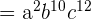
Example 2
Simplify 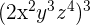
Solution
We will use the exponent power rule here which says that power of the power in the expressions are multiplied together. Remember that in the above expression, we also have 2 and it has no power. Hence, we will take cube of it when we will simplify the expression:


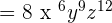
Example 3
Simplify 
Solution
In this expression, the exponents with similar bases are multiplied together, so first we will use the exponent product rule here which says that when two exponents with similar bases are multiplied together, their exponents are added up and the bases remain the same:

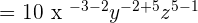
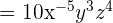
Now, we will use the negative exponent rule here which says that when we have a negative exponent in the numerator or denominator, we can make it positive by shifting its position. Here, x has a negative exponent -5, therefore, we will move it in the denominator to make the exponent or power positive:

Example 4
Simplify 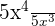
Solution
In this expression, we have the same bases in the numerator and the denominator. We can use the exponent quotient rule here to simplify the expression. The exponent quotient rule says that if two bases are the same and they are divided by each other, then we can keep the base as it is and take a difference of their exponents.
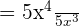

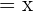
Example 5
Simplify 
Solution
In this expression, two fractions are multiplied with each other. We can use the exponent quotient rule here to simplify the expression. The exponent quotient rule says that if two bases are the same and they are divided by each other, then we can keep the base as it is and take a difference of their exponents.

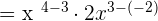

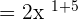
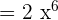
Example 6
Simplify the expression 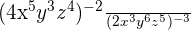 .
.
Solution
First, we will use the exponent power rule here by multiplying the powers with each other:
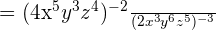
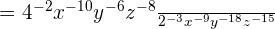
The exponents in the numerator as well as the denominator are negative. Hence, we will invert this equation to make the exponents positive like this:

Now, we will use the exponent quotient rule here which says that when two exponents with same bases are divided by each other, then we can keep the base as it is and take the difference of the exponents:
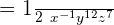
Now, we will again use the negative exponent rule because the power of x is negative:














