Chapters

The best Maths tutors available
What are Radicals?
The radical is also known as a root and it is the inverse operation of applying exponent. It means that we can remove power by taking a radicals and we can remove a radical by taking power. For example, if we take a square of 4, we will get 16 and when we will take a square root of 16, we will get 4. Similarly, if we take the cube of 2, we will get 8 and if we will get a cube root of 8, we will get 2. Mathematically, we can write these examples like this:
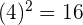 ,
, 
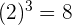 ,
, 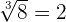
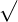 is the radical symbol and the number inside this symbol is known as the radicand. We can read the expression
is the radical symbol and the number inside this symbol is known as the radicand. We can read the expression  as square root 16, root 16, or radical 16.
as square root 16, root 16, or radical 16.In the next section, we will discuss how to multiply radical expressions.
Multiplying Radicals
We can apply the operations of addition, subtraction, multiplication, and division on radicals just like numbers. Radicals are multiplied together by multiplying their radicands (the terms inside the radical symbol). The product of radicands is kept under the same radical sign. Now, let us see how to multiply radicals practically through a couple of examples.
Example 1
Multiply 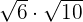
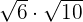
Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 6 and 10. The product of 6 and10 is equal to 60. Hence, the final answer will be:
= 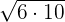
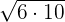
= 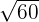
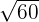
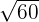 can be simplified further because 60 is equal to 2 x 3 x 5 x 2.
can be simplified further because 60 is equal to 2 x 3 x 5 x 2.= 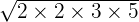
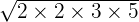
= 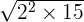
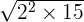
= 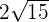
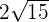
Example 2
Multiply 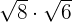
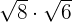
Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 8 and 6. The product of 8 and 6 is equal to 48. Hence, the final answer will be:
= 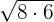
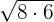
= 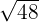
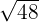
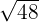 can be simplified further because 48 is equal to 2 x 2 x 2 x 2 x 3.
can be simplified further because 48 is equal to 2 x 2 x 2 x 2 x 3.= 

= 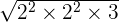
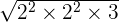
= 

Example 3
Multiply 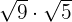
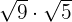
Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 9 and 5. The product of 9 and 5 is equal to 45. Hence, the final answer will be:
= 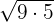
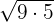
= 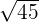
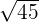
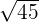 can be simplified further because 45 is equal to 3 x 3 x 5.
can be simplified further because 45 is equal to 3 x 3 x 5.= 

= 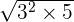
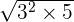
= 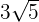
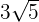
Example 4
Multiply 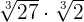
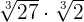
Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 27 and 2. The product of 27 and 2 is equal to 54. Hence, the final answer will be:
= 

= 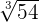
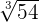
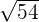 can be simplified further because 54 is equal to 3 x 3 x 3 x 2.
can be simplified further because 54 is equal to 3 x 3 x 3 x 2.= 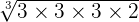
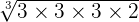
= 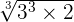
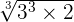
= 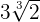
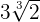
Example 5
Multiply 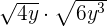
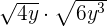
Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 4y and  . The product of 4y and
. The product of 4y and  is equal to
is equal to 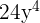 . Hence, the final answer will be:
. Hence, the final answer will be:
 . The product of 4y and
. The product of 4y and  is equal to
is equal to 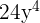 . Hence, the final answer will be:
. Hence, the final answer will be:= 

The answer can be simplified further because 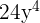 is equal to
is equal to  .
.
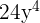 is equal to
is equal to  .
.= 

= 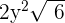
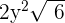
Example 6
Multiply 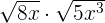
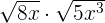
Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 8x and 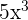 . The product of 8x and
. The product of 8x and 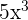 is equal to
is equal to 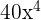 . Hence, the final answer will be:
. Hence, the final answer will be:
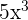 . The product of 8x and
. The product of 8x and 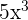 is equal to
is equal to 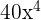 . Hence, the final answer will be:
. Hence, the final answer will be:= 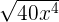
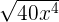
The answer can be simplified further because 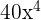 is equal to
is equal to  .
.
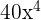 is equal to
is equal to  .
.= 

= 

Example 7
Multiply 

Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 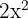 and
and  . The product of
. The product of 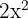 and
and  is equal to
is equal to 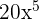 . Hence, the final answer will be:
. Hence, the final answer will be:
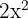 and
and  . The product of
. The product of 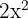 and
and  is equal to
is equal to 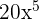 . Hence, the final answer will be:
. Hence, the final answer will be:= 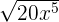
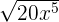
The answer can be simplified further because 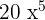 is equal to
is equal to 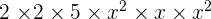 .
.
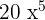 is equal to
is equal to 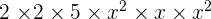 .
.= 

= 

Example 8
Multiply 

Solution
 is equal to 2. Hence, 2 multiplied by
is equal to 2. Hence, 2 multiplied by 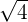 is equal to 4. It can be written as:
is equal to 4. It can be written as:= 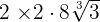
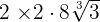
= 

Example 9
Multiply 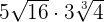
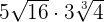
Solution
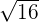 is equal to 4. Hence, 5 multiplied by
is equal to 4. Hence, 5 multiplied by  is equal to 20. It can be written as:
is equal to 20. It can be written as:= 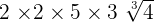
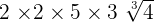
= 

Example 10
Multiply 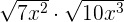
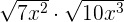
Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 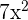 and
and  . The product of
. The product of 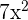 and
and  is equal to
is equal to 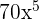 . Hence, the final answer will be:
. Hence, the final answer will be:
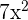 and
and  . The product of
. The product of 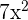 and
and  is equal to
is equal to 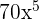 . Hence, the final answer will be:
. Hence, the final answer will be:= 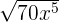
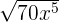
The answer can be simplified further because 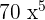 is equal to
is equal to  .
.
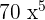 is equal to
is equal to  .
.= 

= 

Example 11
Multiply 

Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 125 and 2. The product of 125 and 2 is equal to 250. Hence, the final answer will be:
= 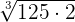
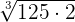
= 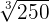
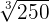
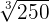 can be simplified further because 250 is equal to 5 x 5 x 5 x 2.
can be simplified further because 250 is equal to 5 x 5 x 5 x 2.= 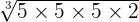
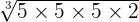
= 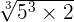
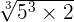
= 

Example 12
Multiply 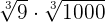
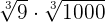
Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 9 and 1000. The product of 9 and 1000 is equal to 9000. Hence, the final answer will be:
= 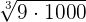
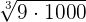
= 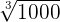
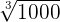
 can be simplified further because 9000 is equal to 2 x 5 x 2 x 5 x 2 x 5 x 3 x 3.
can be simplified further because 9000 is equal to 2 x 5 x 2 x 5 x 2 x 5 x 3 x 3.= 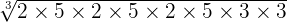
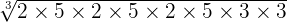
= 

= 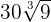
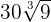
Example 13
Multiply 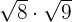
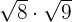
Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 8 and 9. The product of 8 and 9 is equal to 72. Hence, the final answer will be:
= 

= 

 can be simplified further because 72 is equal to 2 x 2 x 2 x 3 x 3.
can be simplified further because 72 is equal to 2 x 2 x 2 x 3 x 3.= 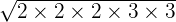
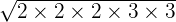
= 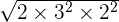
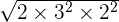
= 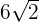
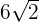
Example 14
Multiply 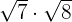
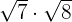
Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 7 and 8. The product of 7 and 8 is equal to 56. Hence, the final answer will be:
= 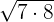
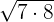
= 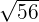
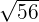
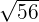 can be simplified further because 56 is equal to 7 x 2 x 2 x 2.
can be simplified further because 56 is equal to 7 x 2 x 2 x 2.= 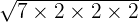
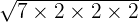
= 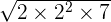
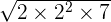
= 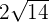
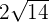
Example 15
Multiply 

Solution
We will simply multiply the terms inside the radical symbol together. The radicands in this example are 8 and 10. The product of 8 and 10 is equal to 80. Hence, the final answer will be:
= 

= 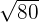
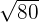
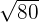 can be simplified further because 80 is equal to 2 x 2 x 2 x 5 x 2.
can be simplified further because 80 is equal to 2 x 2 x 2 x 5 x 2.= 

= 

= 














