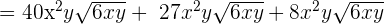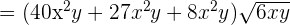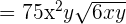Chapters
In this article, we will discuss what are radicals and how to add them.

What are Radicals?
Just like addition is an inverse operation of subtraction and division is inverse of multiplication, a radical or root of a number is inverse if an exponent. The square root is the smallest radical and is expressed by the symbol  . The radical expression bigger than the square root is a cube root which is denoted by the symbol
. The radical expression bigger than the square root is a cube root which is denoted by the symbol 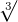 The small number before the radical symbol is known as its index. Index (plural indices) of the radical is also known as an exponent of the radical and it can be used to cancel out the radical function. For example, if an index of the square root is 2, then it can cancel out the root function. The number inside the radical symbol is known as a radicand. For instance, in the expression
The small number before the radical symbol is known as its index. Index (plural indices) of the radical is also known as an exponent of the radical and it can be used to cancel out the radical function. For example, if an index of the square root is 2, then it can cancel out the root function. The number inside the radical symbol is known as a radicand. For instance, in the expression 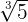 , 5 is the radicand.
, 5 is the radicand.
Some General Rules of Radical Expressions
Some general rules of the radical functions are given below:
- The result of the radical operation is a non-negative, i.e. a positive number if the number inside the radical symbol is positive.
- The result of the radical operation is negative if the number inside the radical symbol is negative or the index of the expression is an odd number.
- If the number inside the radical symbol is negative and the index or exponent of the expression is an even number, then the result of the expression is an irrational number.
Adding Two Radical Expressions
Two radical expressions can be added or subtracted only if they have the same index and the radicand. For instance, consider the following three radicals with same index k and the radicand a:
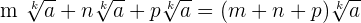
Example 1
Simplify 
Solution
To add the above radicals, first, we will see whether the index and the radicands are the same or not. In the above example, the index of all three radical expressions is 4 and the radicand is 5. Hence, we know that we can add these radicals.
= 
= 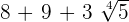
= 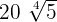
Example 2
Simplify 
Solution
To add the above radicals, we will see whether the index and the radicands are the same or not. In the above example, the index of all three radical expressions is 3 and the radicand is 4. Hence, we know that we can add these radicals.
= 
= 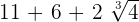
= 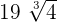
Example 3
Simplify 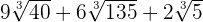
Solution
To add the above radicals, we will see whether the index and the radicands are the same or not. In the above example, the index of all three radical expressions is the same, i.e. 3, however the radicands are different. In this case, we will see whether we can make the radicands the same or not.
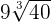 can be written as
can be written as 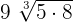 . Simplifying it further will give us the following expression:
. Simplifying it further will give us the following expression:
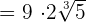

 can be written as
can be written as 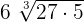 . Simplifying it further will give us the following expression:
. Simplifying it further will give us the following expression:
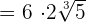
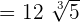
Now, all three radical expressions have the same radicand and same index, so we can easily add them:
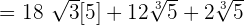
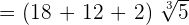
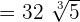
Example 4
Simplify 
Solution
To add the above radicals, we will see whether the index and the radicands are the same or not. In the above example, the index of all three radical expressions is the same, i.e. 2, however the radicands are different. In this case, we will see whether we can make the radicands the same or not.
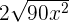 can be written as
can be written as  . Simplifying it further will give us the following expression:
. Simplifying it further will give us the following expression:

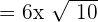
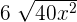 can be written as
can be written as 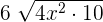 . Simplifying it further will give us the following expression:
. Simplifying it further will give us the following expression:


Now, all three radical expressions have the same radicand and same index, so we can easily add them:

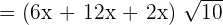

Example 5
Simplify 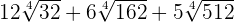
Solution
To add the above radicals, we will see whether the index and the radicands are the same or not. In the above example, the index of all three radical expressions is the same, i.e. 4, however the radicands are different. In this case, we will see whether we can make the radicands the same or not.
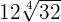 can be written as
can be written as 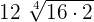 . Simplifying it further will give us the following expression:
. Simplifying it further will give us the following expression:


 can be written as
can be written as 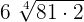 . Simplifying it further will give us the following expression:
. Simplifying it further will give us the following expression:

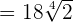
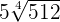 can be written as
can be written as 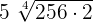 . Simplifying it further will give us the following expression:
. Simplifying it further will give us the following expression:


Now, all three radical expressions have the same radicand and same index, so we can easily add them:
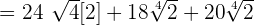
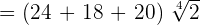
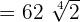
Example 6
Simplify 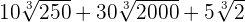
Solution
To add the above radicals, we will see whether the index and the radicands are the same or not. In the above example, the index of all three radical expressions is the same, i.e. 3, however the radicands are different. In this case, we will see whether we can make the radicands the same or not.
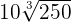 can be written as
can be written as 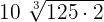 . Simplifying it further will give us the following expression:
. Simplifying it further will give us the following expression:
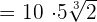
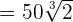
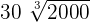 can be written as
can be written as 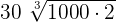 . Simplifying it further will give us the following expression:
. Simplifying it further will give us the following expression:
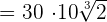
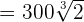
Now, all three radical expressions have the same radicand and same index, so we can easily add them:
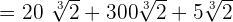


Example 7
Simplify 
Solution
Take the L.C.M of the numbers in the denominator. The L.C.M of 5 and 2 is 10. Hence, we can write it as:
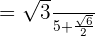
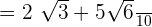
Example 8
Simplify 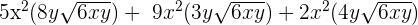 .
.
Solution
First, simplify the above expression like this: