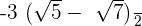In this article, we will discuss how to simplify the radical expressions using the radical formulas. But before proceeding to formulas, first, let us see what are radical expressions.

What are Radical Expressions?
Radicals also known as roots are the inverse of exponents. We denote a radical expression by the symbol 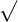 . We can define a radical expression like this:
. We can define a radical expression like this:
A radical expression can be represented as
, where
and
.
Here, N represents natural numbers and R represents real numbers. When "m" in the above radical expression is negative, the value of "n" must be odd. In the above radical expression, "m" represents radicand and "n" is the index of the radical expression.
We can remove a radical sign by taking power and remove the exponent by applying radical. For instance, the cube of 3 is 27, and cube root of 27 is 3. Similarly, the square of 8 is 64 and the square root of 64 is 8.
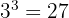

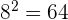

In the next section, we will discuss some of the rules of radical expression which are quite useful in simplifying the expressions.
Radical Formulas
Some of the radical rules are given below:
1. When a radical expression is written in an exponential form, then the index of the radical becomes the denominator of the index of exponential function and power of the radicand becomes the numerator of the index of the exponential function. Mathematically, we can denote it like this:
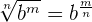
For example, consider the following radical expression.
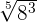
It can be written as:
= 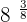
2. Both of the following radical expressions are equivalent.
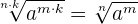
For example, consider the following radical expression:

The above expression is equivalent to the following expression:
= 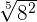
3. The radical expression of the form 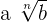 is equivalent to
is equivalent to  .Mathematically, we can write it as:
.Mathematically, we can write it as:
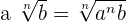
For example, consider the following radical expression:
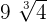
The above expression is equivalent to the following radical expression:
= 
4. Two radical expressions can be multiplied with each other like this:

For example, consider the following radical expression:
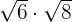
The above radical expression can be written like this:
= 
5. If we have a radical expression of the form 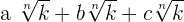 , then we can write it as:
, then we can write it as:
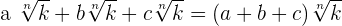
For example, consider the following radical expression:
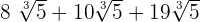
The above radical expression can be written as:
= 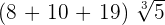
6. When we have two radical expressions with same indices in the numerator and the denominator, then we can write the expression as:

For example, consider the following radical expression:

The above expression is equivalent to the below expression:
= 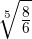
7. If we have a radical expression within a root, then we can write it in simplified form like this:

For example, consider the following radical expression:
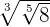
The above radical expression can be written as:
= 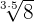
In the next section, we will discuss what is rationalization and its three forms.
Rationalization
Rationalization can be defined as:
Eliminating imaginary numbers or radicals from the denominator in such a manner that the denominator becomes a rational number
When we eliminate radicals from the denominators of the fractions, then we can easily add, subtract, multiply and divide the fractions.
The radical expression can exist in the denominator in three forms. For each of these three form, a different procedure is followed to rationalize the denominator. These three forms are discussed below along with the examples.
First Form
A fraction of the form  is rationalized by multiplying and dividing the expression with the root of the denominator. To rationalize the expression,
is rationalized by multiplying and dividing the expression with the root of the denominator. To rationalize the expression,  , we will multiply and divide it by
, we will multiply and divide it by 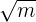 like this:
like this:
= 
= 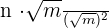
= 
Consider the following example.
Solve 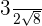 .
.
For rationalization, we have to multiply and divide the above expression by the root present in the denominator. In the above example, the root in the denominator is  . Hence, we will multiply and divide
. Hence, we will multiply and divide 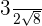 by
by  like this:
like this:
= 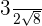
= 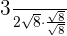
= 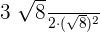
= 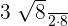
= 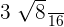
 is equal to
is equal to  . Hence, we can simplify the above expression further like this:
. Hence, we can simplify the above expression further like this:
= 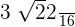
= 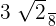
Second Form
A fraction of the form 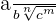 is rationalized by multiplying the numerator and denominator by
is rationalized by multiplying the numerator and denominator by 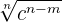 .
.
Consider the following example.
Simplify 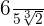
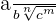 , we will multiply the numerator and denominator by
, we will multiply the numerator and denominator by 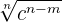 . In the above example, we have to rationalize the fraction
. In the above example, we have to rationalize the fraction 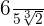 , hence we will multiply the numerator and denominator by
, hence we will multiply the numerator and denominator by 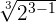 like this:
like this: = 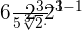
= 
= 
= 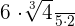
= 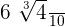
= 
Third Form
A fraction of the form  can be rationalized by multiplying and dividing it by
can be rationalized by multiplying and dividing it by 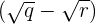 like this:
like this:
= 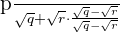
If there is a negative sign between the expression in the denominator, then we rationalize it by inverting the sign.
Consider the following example.
Simplify 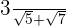
The expression of the type  is rationalized by multiplying and dividing the numerator by
is rationalized by multiplying and dividing the numerator by  .
.
= 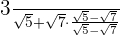
= 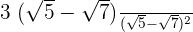
= 
= 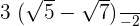
=