In this article, we will explain the concepts related to real numbers in detail.

What are Real Numbers?
In the number system, the real numbers are a mixture of rational and irrational numbers. These numbers can be represented on a number line and we can apply the arithmetic operations of addition, subtraction, multiplication, and division on these numbers. On the other hand, the imaginary numbers 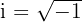 that are part of the complex numbers and can neither be classified as real numbers nor they can be represented on a number line. Complex numbers are formed by multiplying a real number with an imaginary number. Summarizing the above discussion, we can define the real numbers as:
that are part of the complex numbers and can neither be classified as real numbers nor they can be represented on a number line. Complex numbers are formed by multiplying a real number with an imaginary number. Summarizing the above discussion, we can define the real numbers as:
A set of numbers formed by combining the rational and irrational numbers. These numbers are denoted by R.
We can say that the set of real numbers is formed through the union of rational and irrational numbers. Real numbers can be positive or negative. Real numbers include all whole numbers, natural numbers, decimals, and even fractions.
What are rational numbers?
A rational number can be written in the form of 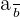 , where
, where  .
.
The examples of rational numbers include  ,
, 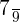 and
and  .
.
What are irrational numbers?
An irrational number cannot be written in the form of 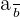 ,where
,where  .
.
In other words, we can say that an irrational number cannot be expressed as a fraction. The examples of irrational numbers include 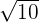 ,
,  and
and 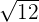 .
.
The following diagram illustrates the set of real numbers which includes both rational and irrational numbers.

We can apply all the operations on real numbers, except for the following three operations:
- The root of an even power
- Negative radicand
- Division by zero
The Real Line
Real numbers can be expressed on a number line where for each real number there is a point that represents that number and for every point on that number line, we have a real number.

The numbers on the right-hand side of the number line are greater than the numbers on the left side. If you have to locate a number on the number line, then you should evaluate the number first. For instance, 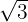 is equal to 1.73 and it is between 1 and 2.
is equal to 1.73 and it is between 1 and 2.
Properties of Real Numbers
The four main properties of real numbers are commutative, associative, distributive and identity property. In this section, we will describe each property in detail.
Commutative Property
Suppose a, b and c are real numbers. The general form of the commutative property will be a + b = b + a for addition and a . b = b . a for multiplication. The examples of the commutative property of addition and multiplication are given below:
Commutative property of addition: 7 + 8 = 8 + 7 , 9 + 2 = 2 + 9
Commutative property of multiplication : 8 x 7 = 7 x 8, 9 x 2 = 2 x 9
Associative Property
Suppose a, b and c are real numbers. The general form of the associative property will be a + (b + c) = (a + b) + c for addition and a(bc) = (ab)c for multiplication. The examples of the associative property of addition and multiplication are given below:
Associative property of addition: 3 + (5 + 9) = (3 + 5) + 9, 7 + (2 + 8) = (7 + 2) + 8
Associative property of multiplication: 2 x (3 x 5) = (2 x 3) x 5, 6 x (7 x 8) = (6 x 7) x 8
Distributive Property
Suppose a, b and c are three real numbers. The distributive property says that a (b + c) = ab + ac and (a + b)c = ac + bc. An example of distributive property is given below:
Distributive property example: 7 (2 + 3) = 7 x 2 + 7 x 3. Both the sides will give the same result.
Identity Property
We have two identities: additive and multiplicative. Additive identity says that if 0 is added to a real number, the answer is the same number. For instance, if a is a real number, then a + 0 = a.
Multiplicative identity says that if 1 is multiplied with a real number, then the result is the number itself. For instance, if a is a real number, then a x 1 = a.
In the next section of the article, we will solve examples related to real numbers.
Example 1
Tell whether the following numbers are real numbers or not along with the reason.
a) 
b) 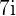
c) 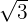
d) 
e) 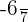
f) 
g) 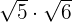
Solution
a)  is not a real number because it is an imaginary number.
is not a real number because it is an imaginary number.
b) 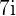 is not a real number because it is formed by multiplying a real number 7 with an imaginary number i. In other words, it is a complex number.
is not a real number because it is formed by multiplying a real number 7 with an imaginary number i. In other words, it is a complex number.
c) 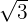 cannot be expressed as a fraction. It is an irrational number. All irrational numbers are real numbers too.
cannot be expressed as a fraction. It is an irrational number. All irrational numbers are real numbers too.
d)  can be written as a fraction. The numbers after the decimal point are repeating in the same pattern, therefore it is a rational number. All rational numbers are real numbers.
can be written as a fraction. The numbers after the decimal point are repeating in the same pattern, therefore it is a rational number. All rational numbers are real numbers.
e) 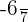 is a fraction. All fractions are rational numbers and all rational numbers are the real numbers.
is a fraction. All fractions are rational numbers and all rational numbers are the real numbers.
f) 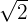 and
and  both are real numbers. The addition and product of two real numbers is also a real number. Hence,
both are real numbers. The addition and product of two real numbers is also a real number. Hence,  is a real number.
is a real number.
g)  and
and 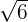 are real numbers and their product will also be a real number.
are real numbers and their product will also be a real number.
Example 2
Consider the following number line and tell which number is greater and why.

a)  and 1
and 1
b) 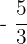 and -2
and -2
c) 0 and 
d) 0 and 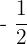
e) -5 and 
f) 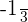 and -0.4
and -0.4
Solution
We will evaluate each number one by one to see which is greatest.
a)  is equal to 1.41. It lies between 1 and 2 on the right side of the 1. Remember that the numbers on the right side are greater than the numbers on the left side of the number line. Hence, we can say that
is equal to 1.41. It lies between 1 and 2 on the right side of the 1. Remember that the numbers on the right side are greater than the numbers on the left side of the number line. Hence, we can say that  is greater than 1.
is greater than 1.
b) 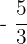 is equal to -1.6. -1.6 lies between -2 and -1. It falls on the right side of -2. Hence, we can say that
is equal to -1.6. -1.6 lies between -2 and -1. It falls on the right side of -2. Hence, we can say that 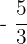 is greater than -2.
is greater than -2.
c)  is equal to 0.5 and it falls between 0 and 1. Since it is on the right side of 0, hence, we can say that
is equal to 0.5 and it falls between 0 and 1. Since it is on the right side of 0, hence, we can say that  is greater than 0.
is greater than 0.
d) 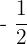 is equal to -0.5. It falls between 0 and -1 and it is located on the left hand side of zero, therefore, 0 is greater than
is equal to -0.5. It falls between 0 and -1 and it is located on the left hand side of zero, therefore, 0 is greater than 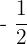 .
.
e)  is equal to 5 and it is clearly greater than -5.
is equal to 5 and it is clearly greater than -5.
f) 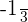 is equal to -0.3. -0.4 is located on the left side of -0.3, hence, we can say that
is equal to -0.3. -0.4 is located on the left side of -0.3, hence, we can say that 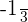 is greater than -0.4.
is greater than -0.4.
Summarise with AI:













