Chapters

Interval Definition
Intervals are a very important idea in mathematics. The basic definition of an interval is the numbers inside of a range. A range is usually made up of two numbers. Take a look at the image below, which gives some real life examples of intervals.

| Interval | Type | |
| A | From 14:00 to 15:00 | Time |
| B | From a grade of F of 0 score to an A of 90 points | Test Scores |
| C | From 18 years old to 64 | Age |
Interval properties
As you saw in the previous section, intervals can be almost anything: time, age, test scores and more. However, there are a few things you should keep in mind when creating your own interval. The most important property of an interval is that it includes all real numbers.
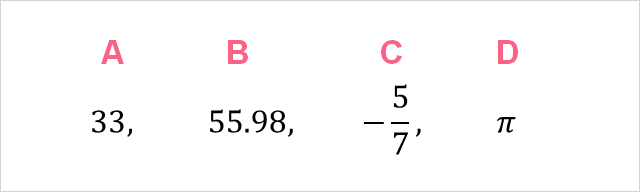
| Type | Explanation | |
| A | Whole number | No decimals, positive |
| B | Rational number | Positive numbers with decimals or fractions |
| C | Rational number | Can also be negative |
| D | Irrational number | Can’t be written as a decimal |
Including Ends
The most important thing to remember is the notation of intervals on the line itself and when written in numbers. On a number line, we usually depict intervals as a straight line with two circles at the end. When the circle is filled in, this means that we want to include that number in our interval.

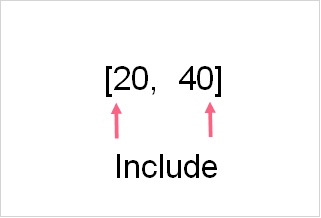
Excluding Ends
When we want to exclude the ends, we can simply leave the circles empty. Let’s take the same example above, only this time, say we only want to include 40.


Inequalities
Inequalities deal with two ideas: greater and less than. The table below shows the definitions of both.
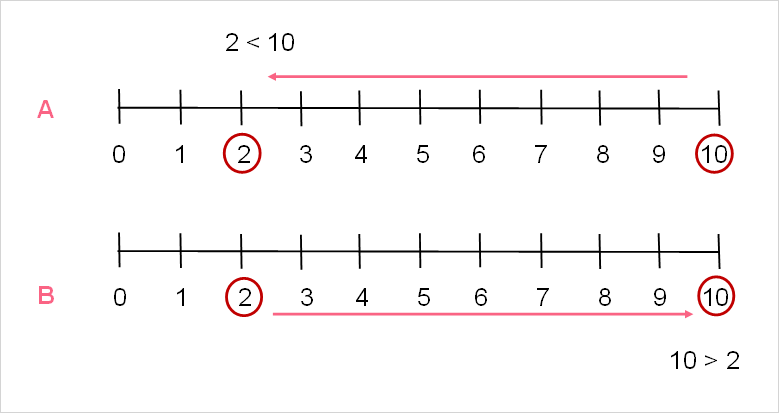
| A | Less Than | < | When a number, x, is to the left of another number, y, on a number line | 2 < 10 |
| B | Greater Than | > | When a number, x, is to the right of another number, y, on a number line | 10 > 2 |
We can also combine inequalities with an equals sign. Check out the possible combinations below.

| A | Less than OR equal to |  | When a number is to the left of or equal to another on a number line | 2  10, 10 10, 10  10 10 |
| B | Greater than OR equal to |  | When a number is to the right of or equal to another on a number line | 10  2, 10 2, 10  10 10 |
Infinity
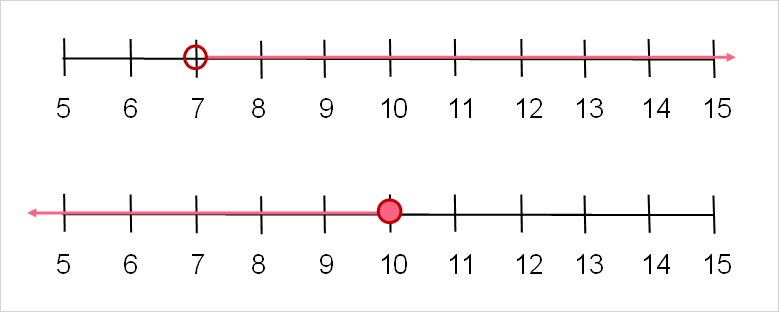
Infinity is something that has no end. Infinity is endless and is a very helpful concept in maths. When we talk about infinity in inequalities, we always exclude infinity. This is because we never reach infinity - it is endless after all!

 ) as another example. When we draw this on a number line, instead of using an empty circle, we simply use an arrow.
) as another example. When we draw this on a number line, instead of using an empty circle, we simply use an arrow.
Notation
Now that we have learned about intervals and inequalities, we can combine both to understand statements of inequalities. Say, for example, that you have a birthday coming up. You know you will get between 100 to 200 pounds from your family and friends. This can be written as:

| A | a < x < b | (a,b) | Exclude a and b |
| B | a > x > b | (a,b) | Exclude a and b |
| C | a  x x  b b | [a,b] | Include a and b |
| D | a  x x  b b | [a,b] | Include a and b |
Union
A union can be thought of as combining several expressions of inequality. The easiest way to understand this is to use infinity. For example, Antoine and Marie are playing a video game where you have positive and negative points. The table describes their possible results.
| Antoine | (-  , 10] , 10] | We know Antoine scored 10 points or less |
| Marie | (7, +  ) ) | We know Marie scored above 7 points |
If we wanted to find the region where they could have tied, we can make a union of these two intervals. A union is written as:

Intersection
An intersection is exactly as it sounds: it is where two things meet. In this case, it is where our two intervals meet. Lets continue from the example above.
Here are the possible scenarios of this game.

| Antoine (A) wins | A = 10 | If Antoine scores 10 points |
| Marie (M) wins | A > 10 | If Marie scores more than 10 points |
| Antoine and Marie tie | 7 < A 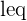 10 10 7 < M | If both Antoine and Marie score above 7 points and 10 points or less |
We can break the table down using the number line.
| A | A < 7 | Antoine loses, as his interval is the only one going below 7 |
| B | 7 < A 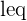 10 10 7 < M | Both Antoine and Marie win, as their intervals both intersect each other between these two points |
| C | M 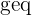 10 10 | Marie wins, as her interval is the only one at 10 or above |
As you can see, the region where they tie is the intersection because it is the interval where both Antoine and Marie’s intervals meet each other. Taking away the A and C parts of the number line, we are left with:

| Notation | Intersection | Description |
7 < x 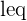 10 10 | (7,10] | Exclude 7 and include 10 |













