Chapters
In this article, we will how to simplify the expressions that contain a radical sign inside a radical. We will also discuss how to simplify nested radicals. But before proceeding to discuss these concepts, first, let us see what are radicals.

What are Radicals?
Radicals are the opposite of exponents and they are also known as roots. We can define a radical function like this:
An algebraic expression that can be written as
, where
and
is known as a radical
Remember that if the value of a is negative, m must be an odd number. Since radical and exponents are inverse to each other, hence we can remove the radical sign by taking an exponent and vice versa. For instance, the square root of 81 is 9 and 9 square is 81. Mathematically, we can denote it as:
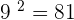
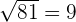
We can read the radical expression  as square root 36, root 36, or simply radical 36. While taking the root of a number, we can go beyond 2. For example, third root, fourth root, fifth root, and so on. The radicals can be converted into powers. For instance,
as square root 36, root 36, or simply radical 36. While taking the root of a number, we can go beyond 2. For example, third root, fourth root, fifth root, and so on. The radicals can be converted into powers. For instance, 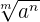 can be written as
can be written as 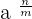 .
.
The symbol 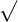 represents a radical and the number inside a radical symbol is known as radicand. The index of the radical is the value above the root symbol. For instance, in the radical expression,
represents a radical and the number inside a radical symbol is known as radicand. The index of the radical is the value above the root symbol. For instance, in the radical expression,  , 3 is known as an index.
, 3 is known as an index.
How to Apply Arithmetic Operations on Radicals?
Just like we can apply the arithmetic operations of addition, subtraction, multiplication, and division on numbers and exponents, we can also apply these operations on radicals. For adding or subtracting the radicals, the numbers within the radical symbol, i.e. the radicand and the index or power of the expression are the same. For multiplication, we simply multiply the terms inside the radical symbol, i.e. the radicands are multiplied with each other. For solving the radical fraction, we need to multiply and divide the expression with a root in the denominator. This process is also known as rationalization.
How to Simplify Radical Expressions?
We can simplify the radicals if:
- The radicand can be converted into an exponent
- We have a fraction inside the radical symbol
- The denominator of the fraction has a radical sign
In the next section, we will discuss what to do when we have a root inside the radical symbol.
Roots of radicals
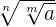

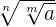 , we had two indices n and m. To simplify the expression, we have multiplied these indices together.
, we had two indices n and m. To simplify the expression, we have multiplied these indices together.What are Nested Radicals?

Example 1
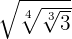
Solution
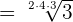

Example 2
Simplify 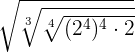
Solution
In this example, we have three indices of the radical expression. These indices are 2, 3 and 4. But before multiplying these indices, first, we will solve the expression inside the radical expression like this:
= 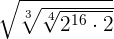
= 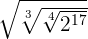
= 
= 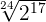
Example 3
Simplify 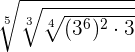
Solution
In this example, we have three indices of the radical expression. These indices are 5, 3 and 4. But before multiplying these indices, first, we will solve the expression inside the radical expression by using the rules of radicals like this:
= 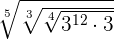
= 
= 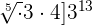
= 
Example 4
Simplify 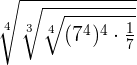
Solution
In this example, we have three indices of the radical expression. These indices are 4, 3 and 4. But before multiplying these indices, first, we will solve the expression inside the radical expression like this:
= 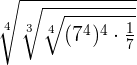
= 
We have the same base 7 in the numerator and denominator of the expression. Hence, we will keep the base as it is and subtract the powers in the final expression.
= 
= 
= 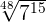
Example 5
Simplify 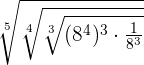
Solution
We have three indices in this example. These indices are 5, 4 and 3. We will multiply these indices while writing the final expression in its most simplified form. But before multiplying the indices, we need to solve the expression inside the root using the rules of radicals:
= 
= 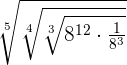
When we have the same base in the numerator and the denominator, then we subtract their powers like this:
= 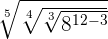
= 
= 
= 
In the next two examples, we will simplify the nested radicals.
Example 6
Simplify 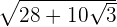
Solution
To solve the above nested radical, we need to assume that it is of the form  . In this example,
. In this example, 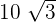 is equal to 2ab. So, a is equal to 5 and b is equal to
is equal to 2ab. So, a is equal to 5 and b is equal to 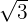 .
.
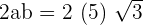
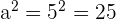
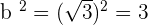
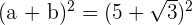
We will substitute this value inside the radical expression like this:
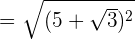
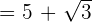
Example 7
Simplify 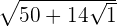
Solution
To solve the above nested radical, we need to assume that it is of the form  . In this example,
. In this example, 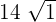 is equal to 2ab. So, a is equal to 7 and b is equal to
is equal to 2ab. So, a is equal to 7 and b is equal to 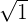 .
.
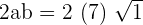
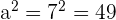
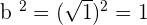

We will substitute this value inside the radical expression like this:
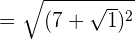

Example 8
Simplify 
Solution
To solve the above nested radical, we need to assume that it is of the form  . In this example,
. In this example,  is equal to 2ab. So, a is equal to 8 and b is equal to
is equal to 2ab. So, a is equal to 8 and b is equal to 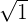 .
.
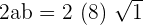

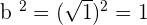
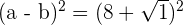
We will substitute this value inside the radical expression like this:

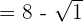
Summarise with AI:












