Chapters

Exercise 1
Classify the following numbers:
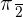

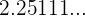
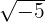
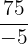
Exercise 2
Represent the following number in the real line:
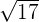
Exercise 3
Represent the numbers that verify the following relations in the real line:
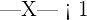



Exercise 4
Calculate the values of the following powers:
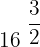
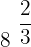

Exercise 5
Represent the following number in the real line:

Exercise 6
Represent the following relations in the real line using real numbers:

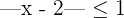

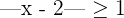
Solution of exercise 1
Classify the following numbers:
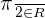
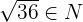
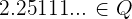

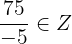
Solution of exercise 2
Represent the following number in the real line:
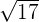
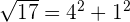
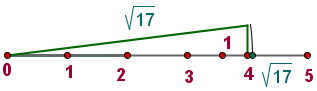
Solution of exercise 3
Represent the numbers that verify the following relations in the real line:









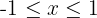



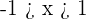

=



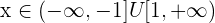

Solution of exercise 4
Calculate the values of the following powers:
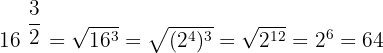
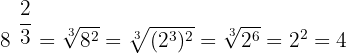
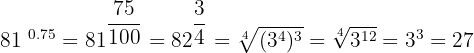
Solution of exercise 5
Represent the following number in the real line:

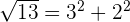

Solution of exercise 6
Represent the following relations in the real line using real numbers:
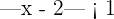
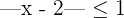
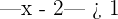
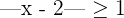
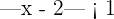
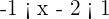
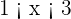
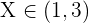




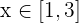

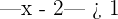
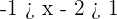
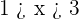


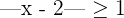




Summarise with AI:













