Chapters
In this article, we will discuss how to rationalize denominators with radicals.

What is Rationalization?
"The process of removing radicals or imaginary numbers from the denominator in such a way that the number in the denominator is converted to a rational number only is known as rationalization"
Removing the radicals from the denominator of the fraction allows us to add, subtract, multiply and divide the fractions in a simple way.
There are three cases when we have a radical in the denominator. We follow different rationalization procedures to remove the radicals in all these three cases. These three scenarios are:
- When we have a fraction of the type

- When we have a fraction of the type

- When we have the fraction

In the next section, we will solve examples in which we will rationalize the fraction belonging to the above three categories.
Example 1
Solve  .
.
Solution
To rationalize the above fraction, we need to multiply and divide the fraction by the root in the denominator. In the above example, the root in the denominator is  . Hence, we will multiply and divide
. Hence, we will multiply and divide  by
by  like this:
like this:
= 
= 
= 
= 
= 
 is equal to
is equal to  . Hence, we can simplify the above expression further like this:
. Hence, we can simplify the above expression further like this:
= 
= 
Example 2
Solve  .
.
Solution
To rationalize the above fraction, we need to multiply and divide the fraction by the root in the denominator. In the above example, the root in the denominator is  . Hence, we will multiply and divide
. Hence, we will multiply and divide  by
by  like this:
like this:
= 
= 
= 
= 
= 
Example 3
Rationalize the following fraction:

Solution
When we get the fraction of the type  , then to rationalize, we multiply the numerator and denominator by
, then to rationalize, we multiply the numerator and denominator by  . In the above example, we have to rationalize the fraction
. In the above example, we have to rationalize the fraction  , hence we will multiply the numerator and denominator by
, hence we will multiply the numerator and denominator by  like this:
like this:
= 
= 
= 
= 
= 
Example 4
Rationalize the following fraction:

Solution
When we get the fraction of the type  , then to rationalize, we multiply the numerator and denominator by
, then to rationalize, we multiply the numerator and denominator by  . In the above example, we have to rationalize the fraction
. In the above example, we have to rationalize the fraction  , hence we will multiply the numerator and denominator by
, hence we will multiply the numerator and denominator by  like this:
like this:
= 
= 
= 
= 
= 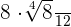
= 
Example 5
Rationalize the following fraction:

Solution
When we get the fraction of the type  , then to rationalize, we multiply the numerator and denominator by
, then to rationalize, we multiply the numerator and denominator by  . In the above example, we have to rationalize the fraction
. In the above example, we have to rationalize the fraction  , hence we will multiply the numerator and denominator by
, hence we will multiply the numerator and denominator by  like this:
like this:
= 
= 
= 
= 
= 
= 
Example 6
Rationalize the following fraction:

Solution
When we get the fraction of the type  , then to rationalize, we multiply the numerator and denominator by
, then to rationalize, we multiply the numerator and denominator by  . In the above example, we have to rationalize the fraction
. In the above example, we have to rationalize the fraction  , hence we will multiply the numerator and denominator by
, hence we will multiply the numerator and denominator by  like this:
like this:
= 
= 
= 
= 
= 
= 
Example 7
Rationalize the following fraction:

Solution
When we get the fraction of the type  , then to rationalize, we multiply the numerator and denominator by
, then to rationalize, we multiply the numerator and denominator by  . In the above example, we have to rationalize the fraction
. In the above example, we have to rationalize the fraction  , hence we will multiply the numerator and denominator by
, hence we will multiply the numerator and denominator by  like this:
like this:
= 
= 
= 
= 
= 
= 
Example 8
Rationalize the following fraction:

Solution
When we have the fraction of the type  , then we rationalize the denominator by multiplying and dividing the numerator by
, then we rationalize the denominator by multiplying and dividing the numerator by  .
.
= 
= 
= 
= 
= 
Example 9
Rationalize the following fraction:

Solution
When we have the fraction of the type  , then we rationalize the denominator by multiplying and dividing the numerator by
, then we rationalize the denominator by multiplying and dividing the numerator by  .
.
= 
= 
= 
= 
= 
Example 10
Rationalize the following fraction:

Solution
When we have the fraction of the type  , then we rationalize the denominator by multiplying and dividing the numerator by
, then we rationalize the denominator by multiplying and dividing the numerator by  .
.
= 
= 
= 
= 
= 
Example 11
Rationalize the following fraction:

Solution
When we have the fraction of the type  , then we rationalize the denominator by multiplying and dividing the numerator by
, then we rationalize the denominator by multiplying and dividing the numerator by  .
.
= 
= 
= 
= 
Example 12
Rationalize the following fraction:

Solution
When we get the fraction of the type  , then to rationalize, we multiply the numerator and denominator by
, then to rationalize, we multiply the numerator and denominator by  . In the above example, we have to rationalize the fraction
. In the above example, we have to rationalize the fraction  , hence we will multiply the numerator and denominator by
, hence we will multiply the numerator and denominator by  like this:
like this:
= 
= 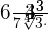
= 
= 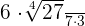
= 
= 













