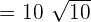Chapters
In this article, you will learn what are radicals, how to add, subtract, multiply and divide them, and how to simplify radical expressions containing powers. But before proceeding to discuss that, first, we will see what are radical expressions.

What are Radicals?
Radical expressions are inverse of exponents and the result of these expressions are roots. In radical expressions, the numbers or coefficients are written inside the radical sign 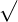 . Radicals are also known as roots. We can convert radical expressions to exponents and exponents into radicals.
. Radicals are also known as roots. We can convert radical expressions to exponents and exponents into radicals.
For example, the square of 9 is 81 and the square root of 81 is 9. Similarly, if we take the square of  , we will get
, we will get  and if we will take the square root of
and if we will take the square root of  , then we will get 5x.
, then we will get 5x.
 as root 25, square root of nine or radical nine. We can also take the powers of the numbers other than two, for instance, 3, 4, 5, 6 and so on.
as root 25, square root of nine or radical nine. We can also take the powers of the numbers other than two, for instance, 3, 4, 5, 6 and so on.How to add, subtract, multiply and divide radicals?
We often come across the fractions that contain radicals in the numerator and the denominator. When the radicals are present in the denominator, then it becomes much easier to simplify the expression by rewriting it in a way that the radical sign is eliminated from the denominator.
Simplifying Radical Expressions
We can simplify a radical expression if:
- The radicand, i.e. the value inside the radical sign can be converted into an exponent
- The radicand is a fraction
- The denominator of a fraction has a radical sign
Let us solve some examples in which we will add, subtract, multiply and divide the radical expressions. In these example, we will also see how to simplify the radical expressions containing powers.
Example 1
Add the following radical expression:
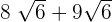
Solution
To add the above expressions, first we will see whether the radicand, i.e. the number inside the radical sign is same or not. In the above case, this number is same, i.e. 6. Hence, we will simply add the number 9 and 8 and keep 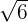 as it is:
as it is:
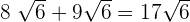
Example 2
Simplify the following radical expression:
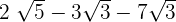
Solution
To subtract the above expressions, first we will see whether the radicands, i.e. the number inside the radical sign is same or not. In the above case, this number is same, i.e. 3 for two terms and it is different for one term. Hence, we will simply evaluate the expressions 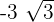 and
and 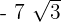 and keep the other term with different radicand
and keep the other term with different radicand 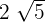 as it is:
as it is:

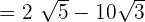
Example 3
Simplify the following radical expression:

Solution
To add or subtract the above expressions, first, we will see whether the radicands, i.e. the numbers inside the radical sign are same or not. In the above case, the number 8 is same for two terms and it is different for one term. Hence, we will simply evaluate the expressions 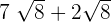 together and simplify
together and simplify 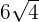 separately:
separately:

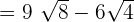
 is equal to 2:
is equal to 2:

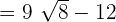
 is equal to
is equal to 


Example 4
Simplify the following radical expression:
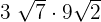
Solution
To multiply the above expression, we will multiply the terms outside the radical sign together. We will repeat the same for the terms inside the radical sign. The resulting answer will be:
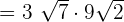

Example 5
Simplify the following radical expression:
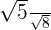
Solution
In this expression, we have got a radical sign in the denominator. Hence, we will use the process of rationalization to simplify this expression. First, we will multiply and divide the expression by the term in the denominator like this:
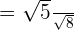
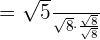
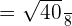
 is equal to
is equal to 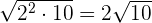 .
.
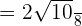
By simplifying it further, we will get the following answer:

Example 6
Simplify the following radical expression:

Solution
In this expression, we have got a radical sign in the denominator. Hence, we will use the process of rationalization to simplify this expression. First, we will multiply and divide the expression by the term in the denominator like this:
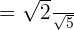

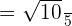
Example 7
Simplify the following radical expression:
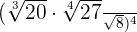
Solution
In the first step, we will apply the power 4 to all the expressions separately like this:
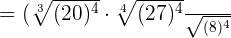
 is equal to
is equal to 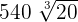
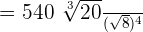
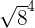 is equal to
is equal to 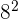 :
:

540 is equal to 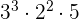
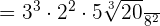
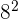 is equal to
is equal to 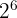

Simplify  like this:
like this:

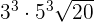 is equal to
is equal to 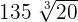 :
:
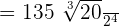
 is equal to 16.
is equal to 16.

Example 8
Simplify the following radical expression:
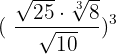
Solution
 is equal to 5 and
is equal to 5 and  is equal to 2:
is equal to 2:
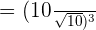
Take the cube of the numerator and the denominator separately like this:
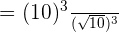
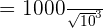
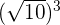 is equal to
is equal to 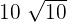

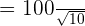
100 is equal to 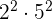 :
:
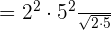

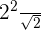 is equal to
is equal to  and
and 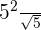 is equal to
is equal to  .
.

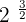 is equal to
is equal to  and
and 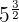 is equal to
is equal to 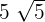 :
:

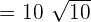
Example 9
Simplify the following radical expression:

Solution
Apply the exponent 3 separately to the numerator and the denominator like this:

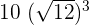 is equal to
is equal to 

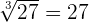
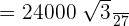
Cancel the common factor 3:
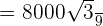

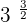 is equal to
is equal to 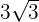 :
:

Example 10
Simplify the following expression:
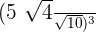
Solution
 is equal to 1000:
is equal to 1000:

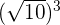 is equal to
is equal to 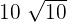

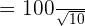
100 is equal to 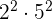 :
:

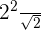 is equal to
is equal to 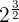 and
and 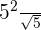 is equal to
is equal to 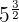 :
:
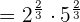
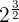 is equal to
is equal to 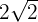 and
and 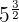 is equal to
is equal to 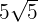 :
:
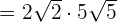
Simplify the above expression by multiplying the radicands and terms outside the radical sign like this: