Chapters
In the previous sections on measures of central tendency and variability, we introduced the definitions and formulas belonging to the most common measures used in descriptive statistics, including mean, standard deviation and variance. Not that common in analysis but still a helpful tool to have is the average deviation. Here, we’ll give a brief overview of the MAD as well as build upon previous sections.

Recap Methods of Variability
Measures of variability are defined as those that calculate the variability, or spread, within a variable or data set. The most common measures of variability are summarized in the table below.
| Measure | Formula |
| Variance | \[ \frac{\Sigma (x_{i} - \bar{x})^2}{n - 1} \] |
| Standard Deviation | \[ \sqrt{ \frac{\Sigma (x_{i} - \bar{x})^2}{n - 1} } \] |
| Interquartile Range | \[ Quartile \thickspace 3 - Quartile \thickspace 1 \] |
| Mean Average Deviation | \[ Mean \; Deviation = \frac{\Sigma | x_{i} - \bar{x} |}{n} \] |
Mean Average Deviation
The average deviation is similar to the standard deviation and is even preferred by many statisticians. However, the average deviation, or MAD, is not a popular measure to report and therefore its use isn’t widespread. As you can see from the formula above, the MAD is the sum of the differences between each observation and the mean divided by the sample size.
For example, take the data table below.
| Observation | Value |
| 1 | 24 |
| 2 | 15 |
| 3 | 8 |
| 4 | 19 |
| 5 | 16 |
The first step in calculating the MAD is to calculate the mean, which can be done as follows.
\[
\bar{x} = \dfrac{24+15+8+19+16}{5}
\]
\[
= \dfrac{82}{5} = 16.4
\]
Next, we follow the formula for the MAD by taking the absolute value of the difference between each data point and the mean.
| Value | \[ | x_{i} - \bar{x} | \] | Result (Rounded to the nearest whole number) |
| 24 | | 24 - 16.4 | | 8 |
| 15 | | 15 - 16.4 | | 1 |
| 8 | | 8 - 16.4 | | 8 |
| 19 | | 19 - 16.4 | | 3 |
| 16 | | 16 - 16.4 | | 0 |
\[
Mean \; Deviation = \dfrac{8+1+8+3+0}{5}
\]
\[
\dfrac{20}{5} = 4
\]
The MAD for the data set is 4, which we interpret as the average absolute difference between mean and each data point.
Average Deviation versus Standard Deviation
There are many differences between the average deviation and the standard deviation. While they both attempt to measure the variability within the data set, they both have a slightly different significance in terms of the data.
Recall that the standard deviation is the measure of variability that tells us how typical a data point is given the mean. The standard deviation is used to understand the probability of a given point being included in a probability distribution.
The average deviation, on the other hand, is an approximate measure of the variability per value within a data set. Meaning, it is an approximate measure of how far away, on average, each value in a data set is from the mean. Take the following data table as an example.
| Observation | Value |
| 1 | 39 |
| 2 | 27 |
| 3 | 36 |
| 4 | 45 |
| 5 | 56 |
| 6 | 68 |
| 7 | 57 |
| 8 | 32 |
| 9 | 29 |
| 10 | 49 |
Let’s find both the standard deviation and average deviation for this data set. The first step for calculating both measures is to find the mean, which can be found below.
\[
\bar{x} = \dfrac{(39+27+36+45+56+68+57+32+29+49)}{10}
\]
\[
\bar{x} = \dfrac{438}{10} = 43.8
\]
The mean is 43.8. Now, to find the standard deviation, we need to subtract the mean from each value. This is actually the same procedure as finding the average deviation. The only difference is that, while the standard deviation squares these subtracted values, the average deviation takes the absolute value of them. Take a look at the table below for a better understanding of what this means.
| Observation | Value | Standard Deviation Formula | Average Deviation Formula |
| 1 | 39 |  | | 39 - 43.8 | |
| 2 | 27 |  | | 27 - 43.8 | |
| 3 | 36 |  | | 36 - 43.8 | |
| 4 | 45 |  | | 45 - 43.8 | |
| 5 | 56 | 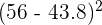 | | 56 - 43.8 | |
| 6 | 68 | 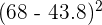 | | 68 - 43.8 | |
| 7 | 57 | 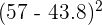 | | 57 - 43.8 | |
| 8 | 32 |  | | 32 - 43.8 | |
| 9 | 29 | 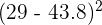 | | 29 - 43.8 | |
| 10 | 49 | 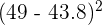 | | 49 - 43.8 | |
| Total | 1661.6 | 112 |
As you can see, the operation is nearly the same. This is because both formulas want to get rid of any negative values. Take, for example, the 9th observation.
\[
29 - 43.8 = -14.8
\]
The negative value here doesn’t indicate what we usually think negative signs indicate. Here, it simply means that 29 is located at a distance of 14.8 below the mean. This is quite a large magnitude, especially when compared to another observation, like the 4th one for example.
\[
45 - 43.8 = 1.2
\]
While traditionally, seeing -14.8 and 1.2 side-by-side would lead us to automatically assume that 1.2 is greater, here we are only interested in the size of the magnitudes. This is why both formulas try to “get rid” of the negative sign by either squaring or taking the absolute value of each magnitude.
Plugging each sum into their respective formulas, we calculate standard deviation as the following.
\[
S = \sqrt{ \frac{1661.6}{10-1}
}
\]
\[
s = 13.6
\]
And the average deviation is calculated as,
\[
Mean \; Deviation = \dfrac{112}{10}
\]
\[
Mean \; Deviation} = 11.2
\]
As you can see, the mean average deviation is less than the standard deviation. This tends to be the case in most data sets. While the standard deviation will be used as a benchmark for how normal a data point is, the MAD can be used to display the average amount of “deviation” from the mean there is in the data set.













Can you help me answer my activities