Chapters
Measures of Central Tendency: Mean, Median and Mode
In the previous chapter, you learned how to identify different types of quantitative variables. In this section, we’ll focus on calculating some of the most common metrics in descriptive statistics, which are mean, median and mode.

What is a Population and Sample?
Today, there are a little over 66 million people living in the UK. By 2100, this number is expected to grow by more than 10 million. With such a diverse and vast population, how is it that we are able to gain information such as the fact that English people drink more tea per person than anyone in the world? Or that there were 29,691 weddings in Scotland for the year 2016? The answer lies in statistics. One of the most important concepts in statistics is the difference between a population and a sample. The definition of a population is that it includes all the units, objects or individuals in the area we want to study.
For example, if we want to know how much tea English people drink, our population would be all of England. If we, instead, wanted to know the amount of tea people drink in London, our population would be the total population of London - roughly 9 million people.
Looking at the population of England, about 56 million people, the idea of taking a survey of all 56 million individuals in our population sounds, and is, impossible. Luckily, statistics has a tool utilized in many disciplines called sampling, which is the act of taking a sample.
The definition of a sample is: a certain number of observations drawn from a population. An observation represents one individual, unit, or object from which you have measured a number of variables. Following our example, instead of trying to measure the tea habits of 56 million individuals making up the English population, we would instead draw a sample from the population totalling, instead, to 40,000 individuals.
An observation, in this case, would be one individual in our sample. For this singular individual, we measured variables such as number of cups per tea had every day, type of tea, if food was eaten with their tea, etc. An easy way to remember what an observation is would be to think about it as what we observe in one unit of our sample.
There are some important differences between a population and a sample. You can find them listed in the table below.
| Population | Sample | |
| Measuring descriptive statistics | Because we can never really know the actual measures in a population, such as mean or variance, we call these characteristics parameters. Parameters are the true measure for a population. | Because our sample is only part of our population, the characteristics we measure from them, such as mean or variance, are called statistic. Sample statistics are our estimations for the true population values. |
| Writing descriptive statistics | The notation for population parameters and sample statistics are different. Here are each differing notations for mean, size. | |
| Mean | \[ \mu \] | \[ \bar{x} \] |
| Size | \[ N \] | \[ n \] |
Simple Random Sampling
In order to draw a sample, statisticians rely on different sampling methods. In most cases, the ideal sampling method is a Simple Random Sample, or SRS. While there are many other methods you can use for drawing a sample from a population, a SRS tends to be desired because of its properties.
SRS involves drawing individuals, objects or units out from a population at random. It assumes that each unit has an equal probability of being chosen. The most common method for drawing a SRS is called the “lottery method.” The general steps for drawing this type of SRS are:
- Choose and define your population
- Number all the people in your population
- Use random selection, such as a random number generator, to pick a number
- The third operation should be repeated until you reach the amount of people you want for your sample
There are also two types of SRS:
- Simple random sampling with replacement
- Simple random sampling without replacement
SRS with replacement is when you replace a unit after you have drawn it. Back to our tea example, let’s pretend we have reduced the population of England 10 people. Each person has been numbered 1 through 10 and all numbers are put inside of a bowl. When performing SRS with replacement, you would pick one number from the bowl, record it, then put it back in the bowl before picking another.
SRS without replacement, on the other hand, means that after picking a number from the bowl, instead of putting it back in, you leave it out and simply pick another one from the bowl. These two methods are easy to remember because, in SRS with replacement, you replace each draw after choosing it. In SRS without replacement, on the other hand, you don’t.
Because this sample is drawn randomly and, in the case of SRS with replacement, are independent from each other, this type of sampling method is highly desired because you are able to apply higher level statistical methods with accuracy. However, SRS methods are often not possible to perform and, in some instances, won’t represent a realistic picture of your chosen population.
Descriptive statistics
Within descriptive statistics, there are two types of measures:
- Measures of central tendency
- Measures of variability
Measures of central tendency attempt to find a central position in the data set. Measures of variability describe how spread the data are from a central point. The most common measures of central tendency are mean, median and mode, which are explained below.
Mean
The definition for the mean is simply the average. To calculate the sample mean, we define the following:
| \[ n \] | The sample size |
| \[ x_{1}, x_{2}, x_{3} \] | The values in the sample |
The formula for finding the sample mean,
\[
\bar{x} = \frac{x_{1}+x_{2}+x_{3}+ \dotsm +x_{n}}{n}
\]
is simply the sum of all the values in our sample over the sample size. It can also be written as,
\[
\bar{x} = \frac{\Sigma \thinspace x}{n}
\]
where the symbol in front of the x, the sigma, means the addition of all x’s, or values in our data.
Median
The definition for the median is simply the midpoint of the data. To calculate the median, you simply arrange all the values in your data in order from least to greatest. Then, you take the middle value of your data.
For even  :
: 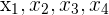
The middle point of the data are 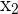 and
and 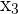 , in this case, you take the average between these numbers:
, in this case, you take the average between these numbers:
\[
\frac{x_{2}+x_{3}}{2}
\]
For odd  :
: 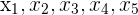
The middle point of the data is simply 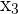
Mode
The definition for the mode is simply the largest occurring value in your data. A common way to remember what mode means is to remember that mode sounds like most. To calculate the mode, you simply see the frequency of each value. The frequency of a value is how many times that value occurs in a data set
For example, let’s say you measure the length of the phones of your friends in centimetres, recorded below.
| Value | Frequency |
| \[ x_{1} = 15 \] | \[ I \thickspace I \thickspace I \thickspace I \thickspace I \] |
| \[ x_{2} = 14 \] | \[ I \thickspace I \thickspace I \] |
| \[ x_{3} = 13 \] | \[ I \thickspace I \thickspace I \thickspace I \] |
In the example above, there are four phones with a length of 15 cm. Because this is the highest frequency, this is the mode.













Can you help me answer my activities