Chapters
In the other sections on this guide on descriptive statistics, we discussed the concept of percentiles. Specifically, we delved into the different types of percentiles statisticians use to investigate their data, how to calculate them and what they are used for. In this section, you’ll find a comprehensive summary of the concept of quartiles.

Raw Scores
Raw scores can sound like an intimidating concept - after all, what exactly makes a score raw? The definition of a raw score is an unaltered data point. Simple! This typically is a quantitative variable and is called a raw score because it is not transformed or modified in any way.
Variable modification comes in many forms and is performed for many reasons. Say, for example, you attain the average speed of cars on a particular street in miles per hour. However, you want to display this mean speed in kilometres per hour - you would then perform a simple operation to covert miles per hour into kilometres per hour. The original measure, miles per gallon, is unaltered - in contrast to the transformed measure in kilometres per hour.
In the case of raw scores, this unaltered datapoint or data set typically applies to some sort of score. This would be something like test scores for example. However, raw scores don’t have to necessarily be scores in the traditional sense.
Transforming a variable isn’t only executed to ease the interpretation or the spread of information. Transformations to a data set or variable also happen to enable the comparison of different data points. One example of this is standardization, where each measure or variable is standardized in order to be able to compare them based off a standard normal distribution.
| Transformation | Description | Example |
| Change of Units | Performing an operation on a variable or value in order to convert it from one unit to another | Changing the variable of weight from pounds to kilograms |
| Creation of a New Variable | Performing an operation on a variable or value in order to create a new variable | Dividing the variable weight from the variable height squared in order to create the variable BMI |
| Standardization | Standardizing the data in order to compare datapoints using a standard normal distribution or a z-table | Standardizing the variable of weight in order to compare how extreme values are given the mean and standard deviation |
| Percentiles | Splitting the data into percentiles in order to compare different segments of the sample | Splitting the data into quartiles in order to compare each 25% segment of the sample |
As you can see from the table above, there are a couple of basic transformations you can perform on a variable.
Percentiles
As mentioned above, percentiles are a type of transformation you can perform on a data set in order to compare different segments of the population. It’s more of a calculation than a transformation, really, but it can be useful to think of it as a tool to perform on a data set.
| Percentile | Value |
| 10th | 150 |
| 50th | 850 |
| 8th | 45 |
| 95th | 1300 |
In the table above, notice that percentiles can take on any value. The data set from which this information came contains data points, whose sample size represents 100% of the sample size, naturally. Percentiles take 1% slices of this sample size, hence the name.
The 8th percentile is nothing more than 8% of the ordered data set. The 50th percentile is 50%, which is also the definition of the median. Between the 95th and 10th percentile lies 85% of the data.
Quartiles
Quartiles are nothing more than a special set of percentiles. As the name suggests, quartiles split the dataset or variable into quarters, or fourths. Quartiles are widely used in statistics because they’re easy to understand and transmit important information about a variable, as can be seen from the table below.
| Quartile | Percentile | Description |
| 0 | 0 | The minimum value of the variable or data set |
| 1st | 25th | 25% of the data are below this point |
| 2nd | 50th | The median of the variable, 50% of the data are below this point |
| 3rd | 75th | 75% of the data are below this point |
| 4th | 100th | The maximum point of the variable |
Notice that the interval between each quartile contains 25% of the data. This can be illustrated in the image below.

Boxplot
Quartiles are an important feature on boxplots. Boxplots are simply another way to represent the distribution of a data set. Similar to histograms, they transmit information about the centre and spread of a variable.
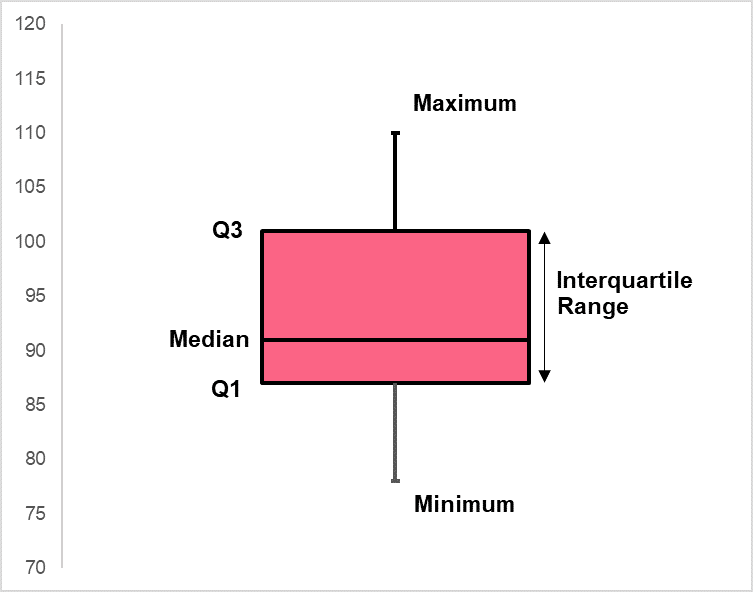
As you can see from the image above, each element of a box plot corresponds to each quartile. Boxplots can be a great tool to analyse the distribution of one variable or for comparison between different variables or categories.
Example
You are interested in understanding how the distribution of ticket sales varies between different months. Interpret the image below using quartiles.

The boxplot above compares the quantitative value of ticket sales across three categories of months. The month of December has a higher median value for ticket sales than January and February. The minimum for ticket sales, however, is highest in January.













Can you help me answer my activities