Chapters
In this section, we will introduce the concept of standard scores, also known as z-scores. We will walk you through the definition and formula for the z-score, as well as provide you with some practice problems.

What is a Z-score?
Think of the sentence: “I have five.” If you were to try and interpret that sentence to someone else, would you be able to do it? Chances are, you would find yourself severely limited in your capacity to explain what “I have five” means without any additional information, the most important one being what exactly someone has five of.
Think of the measures within statistics in this way. You can calculate the mean or variance of a data set, but reporting simply one measure as, for example, “the mean is 50,” doesn’t actually tell us much. As is the case with language, statistics should be reported in the full context of other measures, visualizations and details.
This is where z-scores come in. The definition of a z-score is that it measures the distance between any data point and the mean in terms of standard deviations. If the concept of this as a “score” is tripping you up, it can be helpful to know what raw scores are.
A raw score is an unaltered observation. Like the mean of 50 in our example, raw scores are simply points within a data set. If you take a test and score 30 out of 100, your raw score is 30 points.
Z-scores take these raw scores and transform them into points on a normal distribution. They do this by standardizing the data, which means transforming the data into the distance away from the mean in standard deviations. For example, take the following distribution on test takers, where the mean is 50 and the standard deviation is 8.
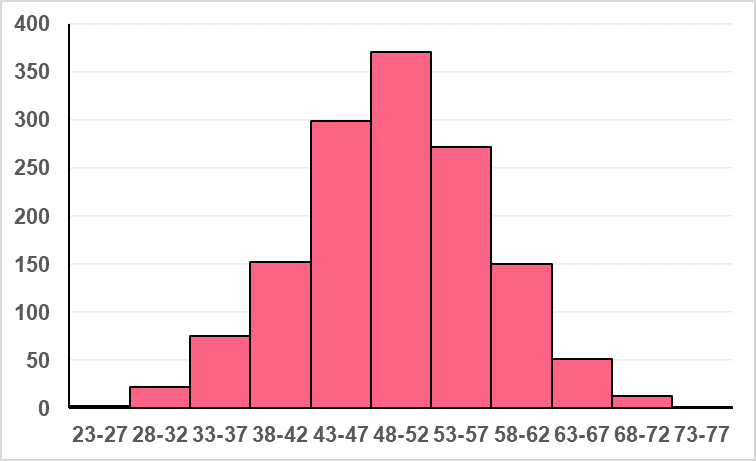
In the image above, we can see that the data seems to follow a normal distribution. If we wanted to analyse the 30 points you scored in the previous example, we would only be able to compare your score to the mean:
- You scored 20 points below the mean
- You scored 30 points out of 100
As you can see, we’re pretty limited in our interpretation. We don’t really have any information to help us understand whether 30 points is a low score or if it was an okay score for this data set. However, transforming the data into z-scores, also known as standardizing the data, we can compare your score on a standard normal distribution. The formula for the z-score is the same as the standardization formula, which is as follows,
\[
z_{i} = \frac{x_{i} - \bar{x}}{s}
\]
Where the notation is written below.
| Notation | Description |
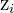 | The z-score of the ith observation |
 | The ith observation |
 | Sample mean |
 | Sample standard deviation |
Following our example, where our  is 50 and our
is 50 and our  is 6, we can calculate the standard score for the 30 points you scored.
is 6, we can calculate the standard score for the 30 points you scored.
\[
z_{i} = \frac{30 - 50}{3} = -2.5
\]
Plotting this on a standard normal distribution, we can see whether or not our value is normal given the mean and standard deviation.

Interpretation of Z-score
As you may have guessed, the interpretation of the z-score is quite simple because of the fact that it doesn’t have any units but, rather, expresses standard deviations. Following our example above, our score is 2.5 standard deviations below the mean. If we had scored points that would have given us a z-score of 2.5 instead of -2.5, we would have been 2.5 standard deviations above the mean.
While the interpretation of the z-score will be different for each individual z-score you calculate, there are some general rules you can follow in order to perform this interpretation. These rules are summarized in the table below.
| Z-Score | Interpretation | Z-score | Interpretation | Z-score | Interpretation | |
| Negative | Below the mean | Zero | Equal to the mean | Positive | Above the mean | |
| Z-Score | Description | Interpretation | ||||
| 1 | Scored 1  away from the mean away from the mean | 68% of the data score 1  below or above the mean below or above the mean | ||||
| 2 | 2  away from the mean away from the mean | 95% of the data score 2  below or above the mean below or above the mean | ||||
| 3 | 3  away from the mean away from the mean | 99.7% of the data score 3  below or above the mean below or above the mean | ||||
| 4 | 4  away from the mean away from the mean | Almost 100% of the data score within 4  from the mean from the mean | ||||
Problem 1
You have the following data on test scores across colleges in the nation. You want to know the approximate number of students that scored 39 points based on the data given
| Observation | Value |
| Mean | 89 |
| Standard Deviation | 25 |
Problem 2
You are trying to understand how hard a particular video game is. You have acquired data on a study conducted on the points scored per half hour of play time. Based on the data below, how would you interpret a z-score of 1? What score would give you that z-score?
| Measure | Value |
| Sample Size | 10 000 |
| Mean | 36 |
| Variance | 2.25 |
| Standard Deviation | 1.5 |
Solution to Problem 1
In this problem, your task was to find out roughly how many students scored 35 points given information about the mean and standard deviation. First, we must find the z-score of 35 points.
\[
z_{i} = \dfrac{39-89}{25} = -2
\]
Following the 66-95-99.7 rule, we know that 2  above and below the mean accounts for 95% of the data. Because the data is symmetrical, we know that on either side of the mean, the -2
above and below the mean accounts for 95% of the data. Because the data is symmetrical, we know that on either side of the mean, the -2  and the 2
and the 2  contain one half of 95%.
contain one half of 95%.
Meaning, the -2  mark signifies,
mark signifies,
\[
\dfrac{95\%}{2} = 47.5%
\]
Meaning, about 47.5% of students scored 35 points, which is 2 standard deviations below the mean.
Solution to Problem 2
In this problem, you were asked to:
- Interpret a z-score of 1 and,
- Find the value that would result in a z-score of 1
To find the z-score that would result in 1, simply isolate the  in the z-score equation.
in the z-score equation.
\[
z_{i} = \frac{x_{i} - \bar{x}}{s}
\]
\[
s* (z_{i}) = (\frac{x_{i} - \bar{x}}{s}) * s
\]
\[
s* (z_{i}) = (x_{i} - \bar{x})
\]
\[
\bar{x} + (s* z_{i}) = x_{i}
\]
Rearranged, the formula becomes:
\[
x_{i} = \bar{x} + (s* z_{i})
\]
Plugging in the values given in the table, we get,
\[
x_{i} = 36 + (1.5* 1) = 37.5
\]
Interpreting this z-score, we would say that about 32.5% of players scored 37.5 points per half hour, which is 1 standard deviation away from the mean.













Can you help me answer my activities