Chapters

Finding Measures of Central Tendency for Weighted Data
In the previous sections dealing with measures of central tendency, you learned the fundamentals of calculating the mean, median and mode as well as how to handle grouped data. We also walked you through the basics of quartiles. Here, we’ll expand upon these topics and show you how to handle weighted data as well as the basics of range.
We’ve all been there: that dreaded question at the end of a test that is impossible to answer and yet is worth so much more than all the questions preceding it. While it may seem like simply another tool designed to make us struggle, making some questions worth more tends to reflect a higher level of complexity.
This is one of the most basic forms of weighting. A weight is assigned to a value to make it worth more or less than other values, hence the term “weight.” Weights are commonly assigned to values in order to give them more or less of an impact on a variable or data set. In statistics, samples or groups within a sample are typically assigned weights in order to correct for errors and variation occurring naturally from sampling methods.
Another basic form of weighting is arriving at a weighted average, discussed in the following paragraphs.
Weighted Mean
Recall that the mean is one measure of central tendency that attempts to give the most typical value of a data set. There are three types of Pythagorean Means:
- Arithmetic
- Geometric
- Harmonic
Here, we’ll deal only with the arithmetic mean, which is simply the mean as you’ve learned it probably dozens of times. The formula for the arithmetic mean of a population and a sample is summarized in the table below.
| Sample | Population |
 |  |
| \[ \bar{x} = \frac{\Sigma x_{i}}{n} \] | \[ \mu = \frac{\Sigma X_{i}}{N} \] |
The formula for the arithmetic weighted mean, on the other hand, is
\[
\bar{x}_{weighted} = \frac{\Sigma (x*w)}{\Sigma w}
\]
The arithmetic mean can also be considered to be a weighted average, where all values have the equal weight of 1. Take the following numbers as an example.
| Value
| Weight
|
| 20 | 1 |
| 10 | 1 |
| 15 | 1 |
| 35 | 1 |
| 20 | 1 |
Where we would calculate the weighted mean as
\[
\bar{x}_{weighted} = \dfrac{(20*1) + (10*1) + (15*1) + (35*1) + (20*1)}{1+1+1+1+1}
\]
Which boils down to the formula for the sample mean,
\[
\dfrac{(20) + (10) + (15) + (35) + (20)}{5}= \frac{\Sigma x_{i}}{n} = \bar{x}
\]
Where the weighted mean diverges from the sample mean is that the weighted mean assigns unequal weights to each value. Meaning, there is at least one weight that’s different from 1. Take the table below as an example.
| Value
| Weight
| Value * Weight
|
| 20 | 0.5 | 10 |
| 10 | 0.6 | 6 |
| 15 | 0.8 | 12 |
| 35 | 1.6 | 56 |
| 20 | 3 | 60 |
Where the weighted mean is calculated as,
\[
\dfrac{(20) + (10) + (15) + (35) + (20)}{(0.5) +(0.6) +(0.8) +(1.6) +(3)}
\]
\[
\dfrac{144}{6.5} = 22.2
\]
Giving us the weighted mean of about 22.
Range
The range in statistics and mathematics is defined simply as the distance between the lowest and highest value of a variable or data set. Taking the example from above, we order it from lowest to highest values.
\[
10, 15, 20, 20, 35
\]
Where the range would simply be,
\[
35 - 10 = 25
\]
While there’s no standard formula for the range, you can think of simply as,
\[
x_{max} - x_{min}
\]
The range is a measure of variability, meaning that it reflects the dispersion of the data set or variable. However, the range is often only used for smaller data sets. This is because the range is sensitive to extreme values. This can easily be seen if we, for example, change the highest value in the example above.
\[
10, 15, 20, 20, 564
\]
Which would now give us a range of
\[
564 - 10 = 554
\]
The range here isn’t such a great indicator as to how the values are spread - in fact, it can often lead to confusion.
You may be wondering why the range is useful at all if it can lead to questionable interpretations of the data. While there are now tons of software tools you can use to churn out more computationally demanding descriptive statistics, such as the standard deviation, the range is still an easy way to understand the dispersion of a data set quickly.
You can also use the Range Rule if you’re in a pinch and don’t have time to perform the calculations necessary for the standard deviation. The range rule states that the standard deviation is approximately four times the range, written as follows.
\[
S \approx \frac{R}{4}
\]
Take the example we used above as an example. Using the formula for the standard deviation, we would have to compute the following.
| Set A | Set B |
| 10 | 10 |
| 15 | 15 |
| 20 | 20 |
| 20 | 20 |
| 564 | 35 |
| Set A | Set B |
| \[ \bar{x} = 125.8 \] | \[ \bar{x} = 20 \] |
| \[ \sqrt{ \frac{\Sigma (x_{i} - \bar{x})^2}{n - 1} } \] \[ \sqrt{ \dfrac{240092.8}{5-1} } \] \[ S = 245 \] | \[ \sqrt{ \frac{\Sigma (x_{i} - \bar{x})^2}{n - 1} } \] \[ \sqrt{ \dfrac{350}{5-1} } \] \[ S = 9.4 \] |
| \[ S \approx \frac{564 - 10}{4} \] \[ = 138.5 \] | \[ S \approx \frac{35 - 10}{4} \] \[ = 6.25 \] |
As you can see, the rough estimate performs better when the data are somewhat more normal. This is because this approximation is based on the 68-95-99.7 rule, where the majority of a normally distributed variable falls within a four standard deviation long perimeter.
Interquartile Range
A better representation of dispersion is the interquartile range, which presents information about the quartiles of the data set. As a brief overview of what quartiles are, explained in more details in other sections of this guide, they involve three basic steps:
- Ordering the variable or data set from the lowest to the greatest values
- Dividing the data into fourths, or quartiles
- Do so by calculating each quartile
The interquartile range is the distance between the third and the first quartile, but should really be thought of as everything between the first and third quartile. Because quartiles, by definition, contain 25% of the data and the interquartile range involves two quartiles, the interquartile range is defined as containing 50%, or half, of the data. Take a look at the image below to see the IQR illustrated.
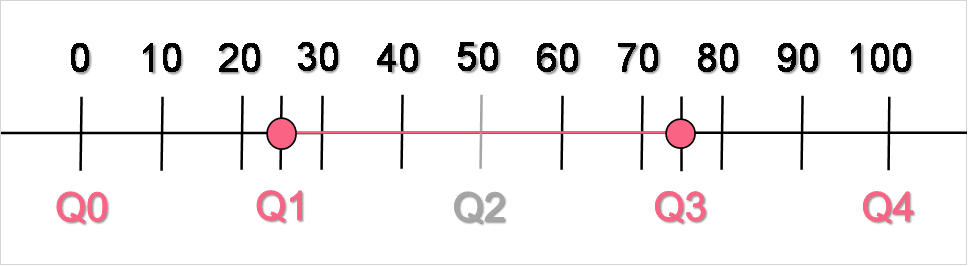
As you can see, the interquartile range falls between the first and third quartiles. The second quartile represents 50% of the data, defined as the median.
Practice Problem 1
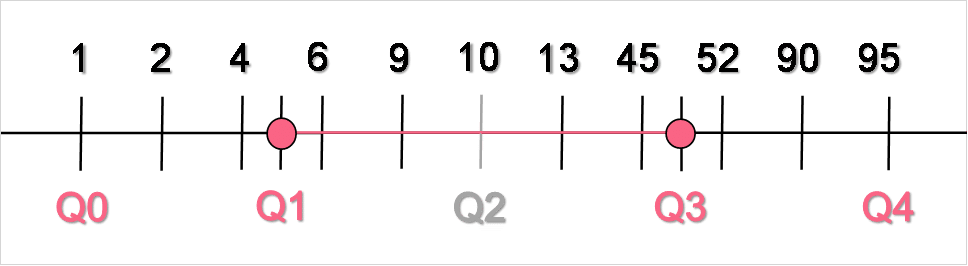
Interpret the quartiles in the image below.
Practice Problem 2
Find the weighted mean of the data set below.
| Value | Weight |
| 20 | 0.3 |
| 40 | 0.1 |
| 10 | 0.4 |
| 60 | 0.6 |
| 30 | 0.7 |
| 55 | 0.2 |
Solution Problem 1
Find the solution in the table below.
| Quartile | Interpretation |
| Q0 | Represents the minimum which is located at 1 |
| Q1 | 25% of the data lie below 5 |
| Q2 | The median, 50% of the data lie above and below 10 |
| Q3 | 75% of data lie below 48 |
| Q4 | Represents the maximum, located at 95 |
Solution Problem 2
Find the solution in the table below.
| Value
| Weight
| Value * Weight
|
| 20 | 0.3 | 6 |
| 40 | 0.1 | 4 |
| 10 | 0.4 | 4 |
| 60 | 0.6 | 36 |
| 30 | 0.7 | 21 |
| 55 | 0.2 | 11 |
| Total | 2.3 | 82 |
\[
\bar{x}_{weighted} = \dfrac{82}{2.3} = 35.7
\]















Can you help me answer my activities