Chapters

Constructing a Pie Chart
In other sections, we showed you the basics of how to display data, also known as data visualizations. These included charts and plots such as bar graphs and histograms. In this section, we’ll go over what a pie chart is, how it’s constructed and in what scenarios it should be used.
What is a Pie Chart?
Pie charts are a given in today’s data friendly environment - chances are, you’ve probably grown up seeing pie charts used in everything from the classroom to television. While it may seem super basic, pie charts are one of the most powerful tools you have to express important characteristics about your data. In 1858, Florence Nightingale produced her infamous “Diagram of the Causes of Mortality in the Army in the East,” known simply as her “Mortality Diagram.”
Looking at a picture of the diagram, you may notice that it looks a lot like a modified pie chart. Nightingale’s interest in both medicine and statistics allowed her to pioneer a new method of data visualization, one which many still consider to be one of the best innovations in the field. Emphasizing that the lack of proper hygiene and facilities was leading to more deaths during the Crimea war than the war itself, Nightingale used what is little more than a pie chart to change public policy for wars in the UK.
The reason behind the pie chart’s strength is its simplicity. Composed of a circle, each section, or “slice,” of the pie chart represents a certain percentage or proportion of the entire variable. You can use a pie chart to display categorical data and their frequencies. Let’s start with an example.
| Number of Cavities | Frequency |
| 0 | 25 |
| 1 | 20 |
| 2 | 35 |
| 3 | 15 |
| 4 | 5 |
Looking at the table above, we can see that it represents a sample of 100 children from a school. The number of cavities indicates how many cavities were found in a child, while the frequencies represent how many children had a certain amount of cavities.
There are two main types of pie charts: a simple pie chart and a pie of pie chart. To build a simple pie chart, you must first find the relative frequency of each value. Discussed in further detail in other sections of our guide to descriptive statistics, relative frequencies are simply the percentage of a value over the total. Meaning, out of a 100 students, only 5 have 4 cavities, so the relative frequency of 4 cavities would be 5 out of 100. In the table below, we’ve calculated the relative frequencies.
| Number of Cavities | Frequency | Frequency in Percentage |
| 0 | \[ \dfrac{25}{100} = 0.25 \] | 25% |
| 1 | \[ \dfrac{20}{100} = 0.2 \] | 20% |
| 2 | \[ \dfrac{35}{100} = 0.35 \] | 35% |
| 3 | \[ \dfrac{15}{100} = 0.15 \] | 15% |
| 4 | \[ \dfrac{5}{100} = 0.05 \] | 5% |
As you can see in the table above, relative frequencies can be and typically are presented as percentages.
Most computer programs will automatically know how to display this information. While it’s unlikely you’ll ever have to draw a precise pie chart by hand, it can help your understanding of them by learning how they are built.
The most basic property of a circle is that it has 360 degrees, where a degree is a unit to measure angles. Having only information about the percentages, we could probably approximate the table into a rough pie chart. However, the way programs do it is by calculating the number of degrees each percentage represents. To do this, you simply multiply the percentage with 360.
| Number of Cavities | Frequency | Frequency in Percentage | Frequency in Degrees |
| 0 | \[ \dfrac{25}{100} = 0.25 \] | 25% | 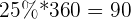 |
| 1 | \[ \dfrac{20}{100} = 0.2 \] | 20% | 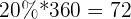 |
| 2 | \[ \dfrac{35}{100} = 0.35 \] | 30% | 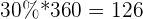 |
| 3 | \[ \dfrac{15}{100} = 0.15 \] | 15% | 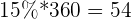 |
| 4 | \[ \dfrac{5}{100} = 0.05 \] | 5% | 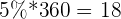 |
The frequency in degrees tell us specific information about the angle of each portion in the pie. Meaning, we now have instructions on how wide each slice of the pie should be. We can now draw our pie chart.
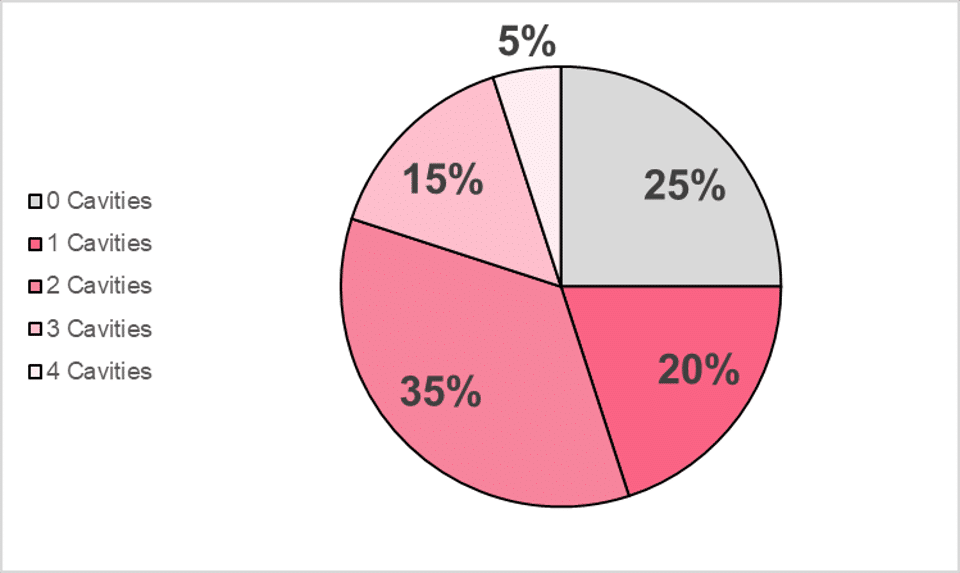
While the table tells us all the information we need to know, visualizing it in this way can be a more effective method of communicating the information. For those who don’t have background in relative frequencies or degrees, the pie chart tells them everything they need to know visually.
Pie of Pie Chart
The second most commonly used pie chart is referred to as a pie of pie chart. This name tells you everything you need to know about what it is. The picture below can help you get a better idea of what this looks like.

Here, you can see that we have two pie charts. On the left, the pie chart represents information about the entire data set. The pie chart on the right, however, represents only the makeup of that single slice, where 20% of the whole data set have 3-4 cavities.
This can be helpful to use when you want to emphasize one component of your data set or when a certain component has multiple parts to it. If this sounds confusing, let’s go back to our cavity example. Let’s say that instead of only 4 cavities, there were up to 10 cavities found in some children in a 1,000 student sample.
| Number of Cavities | Frequency | Frequency in Percentage |
| 0 | \[ \dfrac{250}{1000} = 0.25 \] | 25% |
| 1 | \[ \dfrac{200}{1000} = 0.2 \] | 20% |
| 2 | \[ \dfrac{350}{1000} = 0.35 \] | 35% |
| 3 | \[ \dfrac{100}{1000} = 0.10 \] | 10% |
| 4 | \[ \dfrac{50}{1000} = 0.05 \] | 5% |
| 5 | \[ \dfrac{30}{1000} = 0.03 \] | 3% |
| 6 | \[ \dfrac{15}{1000} = 0.015 \] | 1.5% |
| 7 | \[ \dfrac{2}{1000} = 0.002 \] | 0.2% |
| 8 | \[ \dfrac{1}{1000} = 0.001 \] | 0.1% |
| 9 | \[ \dfrac{1}{1000} = 0.001 \] | 0.1% |
| 10 | \[ \dfrac{1}{1000} = 0.001 \] | 0.1% |
While we want to display the data for cavities, we might want to display this information in a more effective way. A pie of pie chart can be more beneficial to use here than a pie chart because we can condense information. This might be better explained through a practice problem.
Problem 1: Pie of Pie Chart Interpretation
Looking at the image below, we can see that we have combined the values for cavities between 4 and 10. Using the information in this image, fill out the missing values in the table provided below.

| Number of Cavities | Frequency | Frequency in Percentage |
| 0 | \[ \dfrac{250}{1000} = 0.25 \] | 25% |
| 1 | \[ \dfrac{200}{1000} = 0.2 \] | 20% |
| 2 | \[ \dfrac{350}{1000} = 0.35 \] | 35% |
| 3 | \[ \dfrac{100}{1000} = 0.10 \] | 10% |
| 4 and above |
Solution to Problem 1
In this problem, you were asked to interpret the pie in pie chart above by filling out the table. We were told that the pie in pie chart combined the data for cavities between 4 and 10. In other words, we grouped cavities 4 and above, which means we simply need to add up all the values starting from 4 cavities.
| Number of Cavities | Frequency | Frequency in Percentage |
| 0 | \[ \dfrac{250}{1000} = 0.25 \] | 25% |
| 1 | \[ \dfrac{200}{1000} = 0.2 \] | 20% |
| 2 | \[ \dfrac{350}{1000} = 0.35 \] | 35% |
| 3 | \[ \dfrac{100}{1000} = 0.10 \] | 10% |
| 4 and above | \[ \dfrac{(150+30+2+1+1+1)}{1000} \] \[= 0.10 \] | 10% |













Can you help me answer my activities