Chapters

Coefficient of Variation
What is the Coefficient of Variation?
While the discipline of statistics can help put data into order, dealing with data can be far from orderly. One of the most common types of analysis employed in fields like history, medicine and psychology, is called meta analysis. At its most basic, meta analysis is a review of a diverse range of studies that have been performed in the past for one subject.
The difficult thing about comparing different studies, or even two sets of data, is the fact that you will rarely get data that posses the same characteristics, such as the units measured, mean or sample size. In this case, you may be thinking comparing two or more data sets by way of standard deviation will solve the problem. Standard deviation measures the spread, after all.
However, the standard deviation is really only good at letting us compare values within the same data set. A more accurate way of comparing two or more data sets is to use the coefficient of variation.
The definition of the coefficient of variation is that it is the ratio between the standard deviation and the mean. The formula for the coefficient of variation is different for samples and a population, seen in the table below.
| CV for the Population | CV for a Sample |
| \[ CV \thickspace = \frac{\sigma}{\mu}*100% \] | \[ CV \thickspace = \frac{s}{\bar{x}}*100% \] |
- The higher the coefficient of variation, the higher the variability of the data set
This means that, when comparing two or more data sets, the one with the highest coefficient of variability can be said to have the highest variation.
Coefficient of Variation versus Standard Deviation:
The easiest way to understand the difference between the standard of deviation and the coefficient of variation is to look at an example. In the table below, you’ll find two data sets on the amount of people that went to the cinema during a given period of time.
Data Set A:
| Day of the Week | Number of People |
| M | 200 |
| T | 500 |
| W | 300 |
| Th | 1000 |
| F | 400 |
Data Set B:
| Day of the Week | Number of People |
| M | 100 |
| T | 300 |
| W | 400 |
| Th | 1000 |
| F | 1500 |
| Sat | 500 |
| Sun | 100 |
Using the formula for the standard deviation and mean, we get
Data Set A:
\[s = 311.4\]
\[ \bar{x} = 480\]
\[ n \medspace (Sample \thickspace size) = 2400 \]
Data Set B:
\[s = 515.9 \]
\[ \bar{x} = 557.1 \]
\[ n \medspace (Sample \thickspace size) = 3300 \]
Looking at the standard deviation, we would only understand the variability within the data set, which is quite high in both data sets. However, if we wanted to compare these two data sets, using the standard deviation would be risky. Data set A and B have different sample sizes and means. The studies also lasted for different amounts of time, where data set A holds weekday values while data set B holds values for the entire week.
Calculating the coefficient of variation for both data sets, we get:
Data Set A:
\[
\dfrac{311.4}{480} = 0.65
\]
Data Set B:
\[
\dfrac{515.9}{557.1} = 0.93
\]
Now, we can see that data set b, because of the higher coefficient of variation, has a higher variability within its data set. We can see this even by looking at the data set itself, where there is a wide variation between each day.
Problem 1: Comparing Coefficients of Variation
Below, you will find the mean and standard deviation of several data sets. You’re interested in comparing each data set – however, each data set has a different mean, standard deviation and sample size. Find the coefficient of variation for each data set in the table below. Round to the nearest tenth.
| Measure | Data Set A | B | C | D |
| Mean | 45 | 60 | 50 | 25 |
| SD | 3 | 11 | 5 | 15 |
| Sample Size | 1 500 | 3 200 | 500 | 2 700 |
Solution to Problem 1
In this problem, you were asked to:
- Find the CV for each data set
In order to do this, we only need to plug the sample standard deviation and mean of each data set into the formula given above.
| Measure | Data Set A | B | C | D |
| Coefficient of Variation | \[ CV \thickspace = \dfrac{3}{45}*100% \] 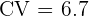 | \[ CV \thickspace = \dfrac{11}{60}*100% \]  | \[ CV \thickspace = \dfrac{5}{50}*100% \] 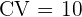 | \[ CV \thickspace = \dfrac{15}{25}*100% \] 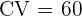 |
In this case, the data set with the lowest CV is data set A, followed by C, D and D. Meaning, set A has the lowest variation amongst these data sets.













Can you help me answer my activities