Chapters

How to Calculate Z-Scores
In other sections of this guide, you learned about the basics of standard scores, including how to calculate them and how they relate to normal distributions. Here, we’ll show you how z-scores are applied in the real world and how you can interpret them in various scenarios.
What is a Z-Score?
As a reminder, standard scores, also known as z-scores, is a score that indicates how usual or typical a data point is within the data set. The z-score uses the mean and standard deviation in order to calculate a score for a data point, letting us know how far away that data point is from the mean in standard deviations.
If this sounds complicated, let’s remind ourselves of what the formula looks like.
| Sample Z-score | Population Z-score |
| \[ z_{i}=\frac{x_{i}-\bar{x}}{s} \] | \[ Z=\frac{x-\mu}{\sigma} \] |
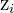 = sample z score = sample z score |  = population z score = population z score |
 = =  observation observation |  = raw score, or observation = raw score, or observation |
 = sample mean = sample mean |  = population mean = population mean |
 = sample SD = sample SD |  = population SD = population SD |
From the sample z-score formula, it’s easy to see that a z score simply measures the distance from a data point to the mean and then divides it by the standard deviation. While the z-score itself can tell you a bit about where the data point lies, it becomes more interpretable after finding that z-score in a z-table.
Finding your z-score on a z-table means finding the corresponding percentage that indicates the proportion of the standard normal distribution that lies below your chosen data point.
Uses of Z-scores
The best thing about standard scores is their simplicity. Because they have the power to tell us how “normal” or typical a value is for a given data set, the applications of z-scores are numerous. From psychology to sports, z-scores are perfect for finding the probability of that data point occurring within a standard normal distribution.
One example of how z-scores are used in the real world comes from the financial world and is called Altman Z-score. While not strictly a z-score in this sense, it does use the concept of the z-score in order to calculate the likelihood of bankruptcy of a company.
The reason why z-scores are so applicable to a diverse range of sectors and subjects is because it:
- Enables people to understand how likely a data point is within a standard normal distribution
- Allows people to compare scores from different samples, which can contain different means and standard deviations
Interpretation of Z-scores
The interpretation of the z-score without a z-table is possible but will limit your interpretation. As a reminder of what the z-score means, recall a normal and standard normal distribution. The only difference between a normal distribution and a standard normal distribution is that, while a normal distribution shows the distribution of a data set following a normal curve, a standard normal distribution expresses the data in terms of standard deviation.


Looking at the images above, we can see the normal histogram on the left side and the standard normal distribution on the right. In the histogram, we can see that the distribution follows a normal distribution curve, with the mean in the centre. What the standard normal curve does is that it standardizes all of these data points.
In other words, all the data points from a normal distribution are taken and standardized. Take a look at the standardization formula and see if you notice where it’s from.
\[
Z=\frac{x-\mu}{\sigma}
\]
That’s right, standardizing any observation is the same as taking the z-score, which means the interpretation is the same as a standard normal distribution. Recall the 68-95-99 rule, which states that:
- 68% of a standard normal distribution have a z-score of -1 to 1
- 95% of a standard normal distribution have a z-score between -2 and 2
- 99% of a standard normal distribution have a z-score between -3 and 3
Interpreting the z-score, then, will follow some general rules expressed in the table below.
| Z-score | Meaning |
| <-1 | 1 SD less than the mean |
| <0 | Less than the mean |
| Equal to 0 | Equal to the mean |
| >0 | Greater than the mean |
| >1 | 1 SD greater than the mean |
This can be extended to z-scores greater or less than 2, 3 and 4.
Z-Score Versus Standard Deviation
While there are many similarities to the z-score and standard deviation, there are major differences between what the two measures are and how they are applied in statistics. The standard deviation, as a brief reminder, is a measure of variability. This means that it strives to measure the dispersion around the mean.
Okay, admittedly this sounds very similar to what the z-score does. However, the main difference stems from the fact that the z-score is a measure of how likely a value is to appear for any given mean and standard deviation.
So, while a standard deviation can tell us information about variability within a data set, the z-score expands this by comparing our data set to a standard normal distribution. This is why the z-score utilizes the standard deviation and mean in order to find out how typical a value is given a standard normal distribution.
Problem 1: Calculating the Z-score
Let’s say that you want to calculate the z-score of a given data set but don’t have information about the mean or standard deviation. In the table below, you have information about the data points within two data sets.
| Observation | Data Set 1 | Data Set 2 |
| 1 | 45 | 11 |
| 2 | 60 | 90 |
| 3 | 74 | 60 |
| 4 | 25 | 45 |
| 5 | 36 | 90 |
Find the z-score of two new data points corresponding to each data set, given below.
| Data Set 1 | Data Set 2 | |
| New Observation | 29 | 150 |
Solution to Problem 1
In this problem, our task was to calculate the z-score of a new observation. First, we need to calculate the mean and standard deviation for each data set. Compare your answers to the table below.
| Data Set 1 | Data Set 2 | |
 | \[ \dfrac{(45+60+74+25+36)}{5} \] \[ \dfrac{240}{5} = 48 \] | \[ \dfrac{(45+60+74+25+36)}{5} \] \[ \dfrac{296}{5} = 59.2 \] |
 | \[ \dfrac{1502}{5-1} = 375.5 \] \[ \sqrt{375.5} = 19.4 \] | \[ \dfrac{4422.8}{5-1} = 1105.7 \] \[ \sqrt{1105.7} = 33.3 \] |
Now that we have the mean and the SD, we can calculate the z-scores for each new value using the formula for standardization. We attain the following result.
| Data Set 1 | Data Set 2 | |
| New Observation | \[ z =\dfrac{(29-48)}{19.4} \] \[ = -0.9805 \] | \[ z =\dfrac{(150-59.2)}{33.3} \] \[ = 2.7307 \] |
| Interpretation | About 1 SD less than the mean | Almost 3 SD above the mean |
Problem 2: Z-Score in the Real World
Z-scores are particularly relevant in situations involving scores. Let’s say you want to calculate how typical your IQ is. You are given the following information about your population’s mean and standard deviation.
| Population | |
 | 100 |
 | 15 |
Pretend that your IQ is 180. How typical is your score compared to the population?
Solution to Problem 2
In this problem, we were asked to:
- Comment on how typical your IQ score is compared to the population
To do this, we must find and interpret the z-score. This is done in the table below.
| Your IQ | |
| z-score | \[ z =\dfrac{(180-100)}{15} = 5.33 \] |
| Interpretation | Your IQ is roughly 5 SD above the population, which happens at a frequency of less than 0.1%. Meaning, this is not typical compared to the population. |













Can you help me answer my activities