Chapters
In this guide on descriptive statistics, we introduced you to the fundamental concepts of descriptive statistics. In this section, we’ll put those skills to the test with a few practice problems. Don’t worry if you’re having trouble remembering certain formulas or ideas, you can always compare your answers to the solutions posted below.

Practice Problems
Problem 1
A study has shown that males in the UK have steadily grown in height from the 1800s to 1980. Based on the data below, find the mean height for each sixty-year period. Then, choose an appropriate chart or plot to visualize this data.
| Year | Height in Cm |
| 1810 | 169.7 |
| 1820 | 169.1 |
| 1830 | 166.7 |
| 1840 | 166.5 |
| 1850 | 165.6 |
| 1860 | 166.6 |
| 1870 | 167.2 |
| 1880 | 168 |
| 1890 | 167.4 |
| 1900 | 169.4 |
| 1910 | 170.9 |
| 1920 | 171 |
| 1930 | 173.9 |
| 1940 | 174.9 |
| 1950 | 176 |
| 1960 | 176.9 |
| 1970 | 177.1 |
| 1980 | 176.8 |
Problem 2
There are multiple data sources on the subject you are currently studying - weights of students in college. You’re interested in data that has low variability and a large sample size, the problem is that the data you found isn’t in kilograms but in pounds. Using variance and standard deviation in pounds (1 kg = 2.20462 lb), which data set out of the following would you choose?
| Measure | Data Set A | Data Set B | Data Set C |
| Sample Size | 15 670 | 4 500 | 9 334 |
| Mean | 550 | 464 | 534 |
| Standard Deviation | 432 | 140 | 210 |
Problem 3
You want to investigate the average amount of time people aged 20 to 40 spend on the phone each week. Interpret the chart below by finding the group mean of the hours spent on the phone.
| Age | Hours |
| 20-22 | 45 |
| 23-25 | 36 |
| 26-28 | 25 |
| 29-31 | 16 |
| 32-34 | 12 |
| 35-37 | 8.5 |
| 38-40 | 4 |

Problem 4
You’re thinking about buying a new computer and are interested in looking at the price of computers on the market. Your budget is between 400 and 600 pounds. What percentage of the computers on the market are between your price range given the information below?
| Mean Price of Computers on the Market | 540 pounds |
| SD of Computers on the Market | 120 pounds |
Problem 5
You are studying the differences of the distributions of streams on a popular music streaming service called Dotify. You find the following chart in a report that studies the number of streams during the first quarter of the year. Interpret the chart using the table provided, measures of central tendency and variability. Keep in mind the data are in thousands.
| January | February | March | |
| Q0 | 90 | 65 | 85 |
| Q1 | 120 | 90 | 115 |
| Q2 | 130 | 100 | 125 |
| Q3 | 140 | 110 | 135 |
| Q4 | 160 | 125 | 155 |

Problem 6
You are studying the frequency of the number of deaths each year for the top 10 causes of death, taken from the World Health Organization. Keep in mind that communicable diseases can pass from individual to individual. Given the following information, interpret the chart below.

| Cause of Death | Type | Frequency (in millions) |
| Ischaemic Heart Disease | Non-communicable | 9433 |
| Stroke | Non-communicable | 5781 |
| Chronic Obstructive Pulmonary Disease | Non-communicable | 3041 |
| Lower Respiratory Infections | Communicable | 2957 |
| Alzheimer Disease and Other Dementias | Non-communicable | 1992 |
| Trachea, Bronchus, Lung Cancers | Non-communicable | 1708 |
| Diabetes Mellitus | Non-communicable | 1599 |
| Road Injury | Injury | 1402 |
| Diarrhoeal Diseases | Communicable | 1383 |
| Tuberculosis | Communicable | 1293 |
Solutions to Practice Problems
Solution Problem 1
Here, we need to:
- Find the mean of each period
- Plot this data
First, we find the mean by applying the formula for the mean,
\[
\bar{x} = \frac{\Sigma x_{i}}{n}
\]
| Year | Height in Cm |
| 1810 - 1860 | \[ \dfrac{169.7+169.1+166.7+166.5+165.6+166.6}{6} = \] \[ \dfrac{1004.2}{6} \] \[ = 167.4 \] |
| 1870 - 1920 | \[ \dfrac{167.2+168+167.4+169.4+170.9+171}{6} = \] \[ \dfrac{1013.9}{6} \] \[ = 169 \] |
| 1930 - 1980 | \[ \dfrac{173.9+174.9+176+176.9+177.1+176.8}{6} = \] \[ \dfrac{1055.6}{6} \] \[ = 175.9 \] |
As we can see, the average height increases over time. This becomes even more apparent when we plot the data.

Solution Problem 2
Here, you were asked to:
- Convert the variance and SD to pounds using the conversion 1 kg = 2.20462 lb
- Choose a data set with low variability and a large sample size
To convert the variance and SD, we simply need to follow the rules for changing units, as seen in the table below.
| Measure | Data Set A | Data Set B | Data Set C |
| Sample Size | 15 670 | 4 500 | 9 334 |
| Mean | \[ \dfrac{550}{2.2} = 250 \] | \[ \dfrac{464}{2.2} = 211 \] | \[ \dfrac{534}{2.2} = 243 \] |
| Standard Deviation | \[ \dfrac{432}{2.2} = 196 \] | \[ \dfrac{140}{2.2} = 64 \] | \[ \dfrac{210}{2.2} = 95 \] |
| CV | 79% | 30% | 39% |
To find a preferred data set, you can use the coefficient of variation. Recall that the formula is,
[\
CV = \frac{s}{\bar{x}} *100%
\]
Which tells us the proportion of the standard deviation to the mean. This is what appears in the last row of the table. Because Data Set C has the second lowest variability but almost double the sample size of Data Set B, we’ll choose Data Set C.
Solution Problem 3
In this problem, in order to interpret the chart you where asked to,
- Interpret the chart by finding the group mean of the hours spent on the phone
To find the group mean, you simply have to follow the formula,
\[
x_{group} = \frac{\Sigma(f_{i}*x_{m})}{n}
\]
| Age | Hours | 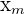 | 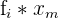 |
| 20-22 | 45 | 21 | 945 |
| 23-25 | 36 | 24 | 864 |
| 26-28 | 25 | 27 | 675 |
| 29-31 | 16 | 30 | 480 |
| 32-34 | 12 | 33 | 396 |
| 35-37 | 8.5 | 36 | 306 |
| 38-40 | 4 | 39 | 156 |
| Total | 146.5 | 3822 |
Plugging this into the formula, you get,
\[
x_{group} = \frac{3822}{146.5} = 26.1
\]
Which means that the group average is ages 26-28. This can be seen in the chart below.

Solution Problem 4
In this problem, you were asked to find:
- The percentage of computers on the market in your price range
To do this, we first have to find the z-scores of the upper and lower limits of our budget. Then, we’ll look these z-scores up in the left-tail z-table to find the percentages these two points represent on a normal distribution.
You’re thinking about buying a new computer and are interested in looking at the price of computers on the market. Your budget is between 400 and 600 pounds. What percentage of the computers on the market are between your price range given the information below?
| Z-Score | Value |
| Lower Limit: 400 pounds | \[ \dfrac{(400-540)}{120} = -1.17 \] |
| Upper Limit: 600 pounds | \[ \dfrac{(600-540)}{120} = 0.5 \] |
Recall that negative z-scores are found by simply taking 1 minus the absolute value of that z-score. Take a look at the image below for more clarification.

Because the distribution is symmetrical, we know that 1 - the right-tail probability is the same magnitude as the negative z-score. Find the z-score in the image below.

Finding the probability of 1.17 in the z-table, we get 0.87900, which gives us the negative probability of,
\[
z_{-1.17} = 1 - 0.87900 = 0.12100
\]
While the z-score for 0.5, looking at the z-table, is 0.69146.
To find the interval of the two probabilities, we simply take the difference between the two. This can be clarified in the image below.

The percentage, then, is,
\[
0.69146 - 0.12100 = 0.57046
\]
Which means about 57% of the computers on the market are within your budget.
Solution Problem 5
In this problem, you were asked to:
- Interpret the chart
Find sample responses in the table below.
| Measure | Interpretation |
| Q0 | January had the highest minimum streams, at 90,000 |
| IQR = Q3 – Q1 | All months had the same IQR of 20,000, which is where 50% of the data lies |
| Q2 | February had the lowest median streams, with 110,000 |
Solution Problem 6
In this problem, you had to,
- Interpret the chart given the data table
Find some sample responses in the table below
| Response | Interpretation |
| Ischaemic heart disease, stroke, chronic obstructive pulmonary disease, dementias, lung cancers and diabetes mellitus make up 77% of the top 10 causes of death | 77% of the top 10 causes of death are made up of non-communicable diseases |
| Road Injury makes up only 5% of the top 10 causes of death | Injury makes up only 5% of the top 10 causes of death in the world |
| Lower respiratory infections, diarrhoeal diseases and tuberculosis make up about 18% of the top 10 causes of death | Communicable diseases make up 18% of the top 10 causes of death |













Can you help me answer my activities