Chapters
In the other sections in this guide on descriptive statistics, we went through the fundamental concepts involved in constructing and interpreting histograms. From understanding the notion of frequencies to the best practices in visualizing data, we will review here all the statistical ideas involved in histograms.

What is a Histogram?
Unless you’ve been living under a rock, you have probably encountered a histogram at some point in your life. In fact, histograms are included in a special offshoot of statistics that involves displaying data in a visual manner instead of simply through numbers and tables.
While tabular and numerical data can be extremely helpful, especially in the other branch of statistics - inferential statistics - data visualization is an integral part of descriptive statistics. This is because seeing a picture of the data can often allow us to recognize patterns we may not have realized were present otherwise.
Histograms make up only a tiny portion of all the types of data visualizations available for people to build. Often, these different visualizations offer a range of advantages and disadvantages given the type of data being presented and the reason for presenting the data. Below, you’ll find a summary of the most common data visualizations.
| Type | Description | Example |
| Pie Chart | For displaying the differing amounts for segments of a whole | A pie chart of the amount of different toppings sold by a pizza restaurant |
| Bar Chart | For displaying different quantitative values of one or more categorical variables | A bar chart showing the amount of snow on the ground for different days of the week |
| Histogram | For displaying different quantitative values for one or more quantitative variables, with zero or more categories | A histogram displaying the distribution of weight across different age groups for males and females |
| Line Graph | For displaying how a quantitative value changes across another quantitative values, with zero or more categories | A line graph showing how weight changes across time for females and males |
How to Build a Histogram
Building a histogram is no longer a question of busting out a ruler and a pencil. In the present day, there are hundreds of programs online as well as computer software dedicated to creating data visualizations. For most of these programs, you simply need to input whatever data you want to display and, in a matter of seconds, a histogram will be built for you.
It can be helpful for the sake of interpretation, however, to understand how a histogram is built. Take the following data as an example, where the data is already grouped into intervals known as “bins” on a histogram.
| Time | Number of Passengers |
| 6:00 - 8:00 | 156 |
| 9:00 - 11:00 | 607 |
| 12:00 - 14:00 | 304 |
| 15:00 - 17:00 | 216 |
| 18:00 - 20:00 | 789 |
| 21:00 - 23:00 | 142 |
| 24:00 - 2:00 | 34 |
It’s helpful to think of the bins of a histograms as bins because they are not static. In computer programs, you can often adjust the width of the bins to include as many or as little data points as you desire.
As you can see by comparing the table above with the histogram below, the frequency of each group corresponds to the height of each bar. It is important to be mindful of the number of bins you choose for your histogram, as choosing too little or too many can result in misleading charts.

Histograms tell us information about the distribution of a variable. Meaning, they summarize information about where the data points of a variable or data set are located. This can be a helpful tool when trying to analyse the spread and centre of a variable.
Histogram versus Bar Chart
Many times, people confuse histograms with bar charts - and it’s not for nothing. Bar charts and histograms have a strikingly similar appearance. Take a look at the image below and try to distinguish which chart is a histogram.

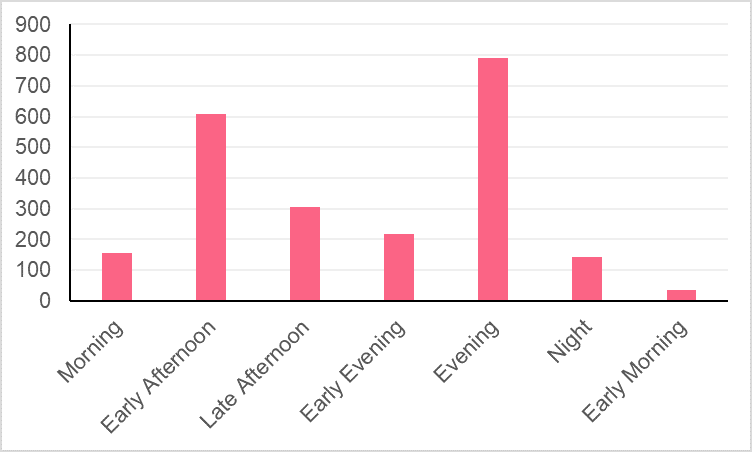
So, what is the difference between a histogram and a bar chart? Taking a look at the image above, you’ll see that the main giveaway is that the bars of a histogram are positioned without any space in between them. This is because, typically, the width of the bars on a histogram represent intervals.
On the other hand, the bars in a bar chart are separate from each other. In addition, the order of the bars on a bar chart doesn’t matter. You can typically rearrange the bars on the horizontal axis of a bar chart with no problems because they usually don’t have a meaningful order. Take a look at the table below, which outlines the major differences between bar charts and histograms.
| Histogram | Bar Chart | |
| Type of Date | Quantitative | Quantitative and qualitative |
| Variables | At least 2 quantitative variables | At least 1 quantitative and 1 qualitative |
| Bars | Bars have no space between them | Bars are separated |
| Interval | Bar width represent intervals | Bar width has no meaning, simply aesthetic |
| Order | Order of bars do matter, have to be arranged in order of intervals | Order of bars don’t matter and can be arranged in any way |
Histogram by Category
While many are probably used to seeing a standard histogram in math or on the news, the structure of histograms is quite flexible. Meaning, histograms don’t strictly have to display information on only one variable. In fact, histograms that display two different variables can often be used to highlight the differences between their distributions.
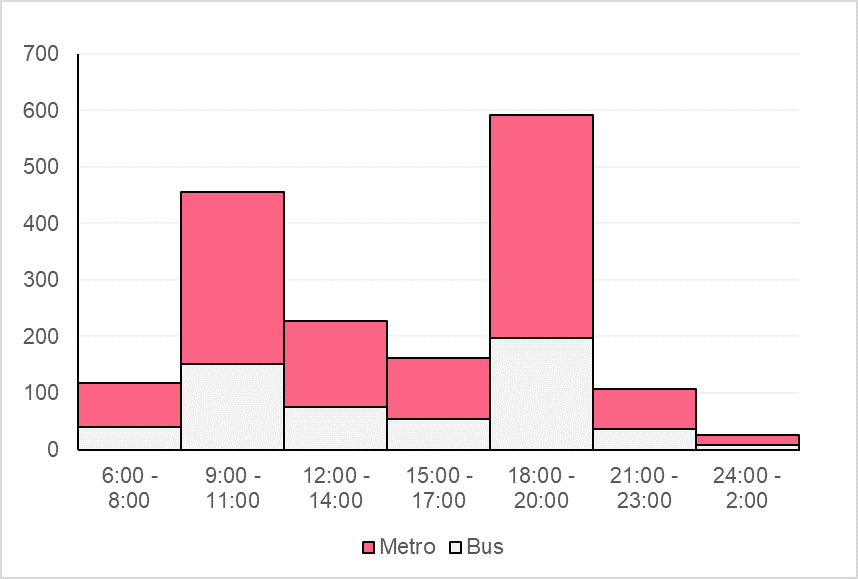
Looking at the image above, you can see how meaningful displaying information of two different categories of the same variable on the same chart can be. This is an example of how histograms can be altered to share more in-depth information about a variable’s distribution. To do this, you will typically need:
- One quantitative variable on the vertical axis
- One quantitative variable split by one qualitative variable (with at least two categories) on the horizontal axis
The flexibility of histograms isn’t limited to simply displaying a quantitative variable by its categories. Histograms can be combined with other charts, such as line graphs or area charts, into what is sometimes called a “combination chart” or a “combo.” Typically, this involves a secondary vertical axis, which renders information about the histogram on one vertical axis and about the other chart or graph on the other.
Measures of Central Tendency on a Histogram
As we mentioned, histograms are typically used to transmit information about a variable’s distribution. This means that the characteristics of a distribution, such as measures of variability and spread, can be viewed on a histogram. Take the picture below as an example.

Here, we know the mean and the median because it is marked on the chart. Typically, you won’t have this information readily available on a histogram and will have to calculate it separately. However, histograms are a great tool to use if you want to get an idea of the centre of the data quickly.
The mode, on the other hand, can almost always be seen from the histogram. While you would technically have to either calculate the group mode or look at the original, ungrouped data set to extract the mode - looking to a histogram can give you a quick estimate. Here, we can see that the mode appears to be in the interval 97-99.
As to the interpretation of histograms, using measures of central tendency and variability can aid in explaining your data to others. Often in statistics, data visualizations are often accompanied by measures such as the mean or standard deviation. This is an integral part of descriptive statistics because it serves to show that all statistical notions are connected.
Example
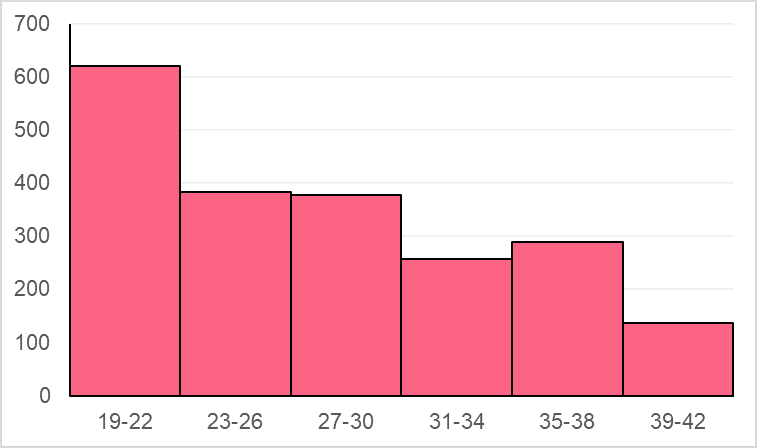
You want to display the distribution of the variable you have studied in an easy-to-comprehend manner. Because you want to express the natural patterns in the distribution of your data set, you don’t want to obscure too much of the data. Given the data table below, what are the number of bins you should use for your histogram?
| Age | Frequency |
| 19 | 240 |
| 20 | 140 |
| 21 | 130 |
| 22 | 110 |
| 23 | 99 |
| 24 | 108 |
| 25 | 106 |
| 26 | 70 |
| 27 | 72 |
| 28 | 99 |
| 29 | 65 |
| 30 | 141 |
| 31 | 43 |
| 32 | 21 |
| 33 | 125 |
| 34 | 68 |
| 35 | 75 |
| 36 | 74 |
| 37 | 87 |
| 38 | 53 |
| 39 | 91 |
| 40 | 45 |
From the picture below, you can see that the answer is 6 bins. While there is, of course, no right or wrong answer, you should understand that some displays are more complete than others. Image a histogram with only 2 bins - this would clearly mean grouping all the data into large intervals that would be difficult to interpret. Choosing too many, however, can get messy and hide important patterns in your data - especially when you deal with larger and larger datasets.













Can you help me answer my activities