Chapters
In previous sections of this guide, you learned how to calculate measures of central tendency and variability. Specifically, we showed you the formulas for mean and variance, how to interpret these measures and why they are used. In this section, we’ll put what you’ve learned to the test with various practice problems meant to challenge and reinforce the knowledge you’ve built.

Mean
As a brief overview of the mean, recall that it is one of the most common measures of central tendency. The mean is defined as an average of a variable or data set and is typically used when there are no extreme values. This is because the mean is sensitive to outliers. Below, you can find the formulas for the various means we’ve explained throughout this guide on descriptive statistics.
| Type of Mean | Formula |
| Arithmetic | \[ \frac{\Sigma x_{i}}{n} \] |
| Geometric | \[ \sqrt[n]{a_{1}*a_{2}*\dotsm*a_{n}} \] |
| Harmonic | \[ H = \frac{n}{\Sigma_{i=1}^{n}{\dfrac{1}{x_{i}}}} \] |
| Weighted | \[ \bar{x}_{weighted} = \frac{\Sigma x_{i}* w_{i}}{\Sigma w_{i}} \] |
| Group | \[ x_{group} = \frac{\Sigma(f_{i}*x_{m})}{n} \] |
Variance
The variance, unlike the mean, is a measure of variability. Meaning, it captures the amount of spread within a variable or data set. Measures of variability are often reported alongside measures of central tendency. Meaning, the variance is typically taken with the mean or the median, as this helps form a greater picture of what the data set looks like. Below are the formulas for the variance.
| Formula | Variance Shortcut | |
| Population Variance | \[ \sigma^2 = \frac{\Sigma(X-\mu)^2}{N} \] | \[ \sigma^2 = square \; of \; sample \; \sigma \] |
| Sample Variance | \[ s^2 = \frac{\Sigma(x_{i}-\bar{x})^2}{n-1} \] | \[ s^2 = square \; of \; sample \; s \] |
Practice Problems
Below, you’ll find practice problems for the mean and variance. Don’t worry if you don’t get the answer right away, you can always compare it to the solutions below.
Problem 1
Find the group mean of the data below.
| Age Group | Frequency |
| 10 - 19 | 3 |
| 20 - 29 | 5 |
| 30 - 39 | 21 |
| 40 - 49 | 19 |
| 50 - 59 | 11 |
| 60 - 69 | 2 |
Problem 2
Find the final grade of this student given the following data.
| Assignment | Value | Weight |
| Homework | 10 | 1.5 |
| Tests | 25 | 0.5 |
| Participation | 7 | 2.3 |
| Final Report | 10 | 5.5 |
Problem 3
Find the geometric mean of the following series.
| Observation | Value |
| 1 | 3 |
| 2 | 9 |
| 3 | 27 |
| 4 | 81 |
| 5 | 243 |
| 6 | 729 |
Problem 4
Given the following information, find the population variance.
| Measure | Value |
 | 50 |
 | 4 |
Problem 5
Find the variance of the following data.
| Observation | Value |
| 1 | 25 |
| 2 | 26 |
| 3 | 38 |
| 4 | 45 |
| 5 | 31 |
| 6 | 30 |
| 7 | 29 |
Problem 6
Calculate the variance of the data sets given the following information.
| Mean | SD | Sample Size | |
| Data Set M | 715 | 55 | 1 500 |
| Data Set D | 634 | 42 | 2 300 |
Problem 7
Interpret the variance and mean given.
| Mean | Variance |
| 24 | 9 |
Solutions to Practice Problems
Below are the solutions to the practice problems above. Make sure to first try them on your own before checking for the solution. If some of the answers are still slightly confusing to you, make sure to review the other sections of our guide dealing with measures of central tendency and variability.
Solution Problem 1
To find the group mean, you simply need to follow the formula,
\[
x_{group} = \frac{\Sigma(f_{i}*x_{m})}{n}
\]
| Age Group | Frequency | 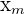 |  |
| 10 - 19 | 3 | 14.5 | 43.5 |
| 20 - 29 | 5 | 24.5 | 122.5 |
| 30 - 39 | 21 | 34.5 | 724.5 |
| 40 - 49 | 19 | 44.5 | 845.5 |
| 50 - 59 | 11 | 54.5 | 599.5 |
| 60 - 69 | 2 | 64.5 | 129 |
| Total | 61 | 2462.5 |
Plugging this into the formula, we get the group mean as,
\[
\dfrac{2464.5}{61} = 40.4
\]
Looking at the chart below, you can see the placement of the mean within the data set.

Solution Problem 2
To find the final grade of this student, we have to find the weighted mean, following the formula,
\[
\bar{x}_{weighted} = \frac{\Sigma x_{i}* w_{i}}{\Sigma w_{i}}
\]
| Assignment | Value | Weight |  |
| Homework | 10 | 1.5 | 15 |
| Tests | 25 | 0.5 | 12.5 |
| Participation | 7 | 2.3 | 16.1 |
| Final Report | 10 | 5.5 | 55 |
| Total | 9.8 | 98.6 |
Plugging this into the formula, we get,
\[
\dfrac{98.6}{9.8} = 10.1
\]
Solution Problem 3
In order to find the geometric mean of the geometric series, we must use the following formula,
\[
\sqrt[n]{a_{1}*a_{2}*\dotsm*a_{n}}
\]
| Observation | Value |
| 1 | 3 |
| 2 | 9 |
| 3 | 27 |
| 4 | 81 |
| 5 | 243 |
| 6 | 729 |
| All values multiplied | 10460353203 |
Plugging this into the formula, we get,
\[
\sqrt[6]{3*9*27*81*243*729} = \sqrt[6]{10460353203} = 46.8
\]
Where we can see the mean plotted in the graph below.
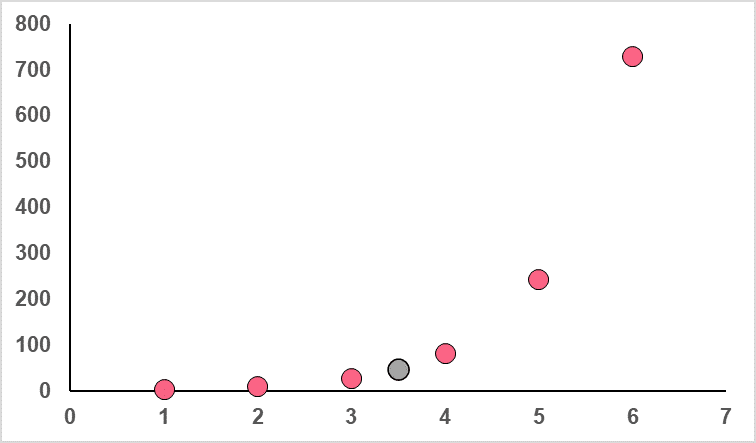
Which may be more clear when plotted on one axis.

Solution Problem 4
We were given information on the population mean and population standard deviation. To find the population variance, simply follow the steps in the table below.
| Measure | Description |
| 1. Remember that the variance is simply the square of the standard deviation | \[ (\sqrt{\sigma^2}) = \sigma \] |
| 2.To find the population variance, simply take the square of the population SD | \[ (\sigma)^2 = \sigma^2 \] \[ 4^2 = 16 \] |
Solution Problem 5
To find the variance of the data, simply follow the formula,
\[
s^2 = \frac{\Sigma(x_{i}-\bar{x})^2}{n-1}
\]
Where the mean is,
\[
\bar{x} = \dfrac{224}{7} = 32
\]
| Observation | Value |  |
| 1 | 25 | 49 |
| 2 | 26 | 36 |
| 3 | 38 | 36 |
| 4 | 45 | 169 |
| 5 | 31 | 1 |
| 6 | 30 | 4 |
| 7 | 29 | 9 |
| Total | 224 | 304 |
Plugging this into the formula, we get,
\[
\dfrac{304}{7-1} = 50.7
\]
Looking at the graph below, we can see the mean and standard deviation plotted.

Which may be more clear when plotted on a single axis.

Solution Problem 6
As in the previous example, we can calculate the sample variance by taking the square of the SD.
| Mean | SD | Variance | |
| Data Set M | 715 | 55 | \[ =55^2 = 3025 \] |
| Data Set D | 634 | 42 | \[ =42^2 = 1764 \] |
Solution Problem 7
Find a sample interpretation below.
Mean: The centre is located at the point 24.
Variance: The spread of the data is relatively small, meaning that the data points are clustered closely around the mean.
This would look something like the following.

A measure of variability is important to report with the mean because it indicates the spread of the data. Take a look at the following data points, which also have a mean of 24 but have a variance of 110.

As you can see, the variance is a great indicator for how close or how far the data points are located about the mean. The general rule is, the larger the variance, the more spread out the data points are. Note that a bigger variance isn’t inherently bad.
For example, if these data points were test scores, as a teacher you would probably prefer the data points with a higher variance. This is because it would be easier to pinpoint which questions and concepts students didn’t understand by taking a look at the students with lower than average test scores, rather than trying to find frequently missed concepts for a test with a cluster of the same grades.













Can you help me answer my activities