Chapters
Visualizing Data Part 2
In previous sections you learned some of the most common methods used in visualizing the measures of central tendency. Namely, we showed you some common tools to visualize data. Here, we’ll expand upon what you’ve learned and show you how to interpret measures of central tendency from histograms and boxplots.

Measures of Central Tendency
There are many measures of central tendency - however, the most common are mean, median and mode. The reason why these are the most common is because they are the simplest to calculate but the most effective to both interpret and relay to someone. In the table below, you’ll find a summary of how to calculate them.
| Mean | Median | Mode | |
| Sample Notation | \[ \bar{x} \] | No standard notation | No standard notation |
| Sample Formula | \[ \bar{x} = \] \[ \frac{\Sigma x_{i}}{n} \] | For odd  \[ x_{1}, x_{2}, x_{3} \] The median is \[ = x_{2} \] For even \[ x_{1}, x_{2}, x_{3}, x_{4} \] The median is \[ = \frac{x_{2}+x_{3}}{2} \] | Highest frequency |
| Population Notation | \[ \mu \] | No standard notation | No standard notation |
| Population Formula | \[ \mu = \] \[ \frac{\Sigma x_{i}}{N} \] | For odd \[ x_{1}, x_{2}, x_{3} \] The median is \[ = x_{2} \] For even \[ x_{1}, x_{2}, x_{3}, x_{4} \] The median is \[ = \frac{x_{2}+x_{3}}{2} \] | Highest frequency |
Recall that measures of central tendency tell us information about the centre of the data set. They are typically used in order to gauge what the most typical value of a data set is. The mean represents the average value of a variable, while the median represents the midpoint of the variable.
The mode, on the other hand, represents the most frequently occurring value in the data set. In other words, the mode represents the highest frequency.
Interpreting Mean, Median and Mode
Measures of central tendency strive to present the centre of the data. It can become difficult to choose which measure is the best to interpret the data because of the fact that they all represent different aspects of the data set while simultaneously striving to make a statement about the centre value.
Recall some general rules of thumb mentioned in previous sections, which stated that:
- If there are outliers or extreme values, the median may be the best measure of central tendency
- If there aren’t any extreme values or outliers, the mean may be the best, especially with large sample sizes
- If the goal is to find the highest frequency, or amount, of a certain variable, the mode will probably be the best measure
When to Use the Mean
The mean should be used above all other measures of central tendency when there aren’t extreme values or outliers and we want to understand the typical value of the data. One example in the real world is when people try to understand averages per country, like height.
Because height tends to have a low level of outliers, we can simply take the average of a sample from a country to determine what the average height of a person there is. Mean is also the measure of central tendency used most when making comparisons over time. It can be visualized in line graphs, bar charts, heat maps and more. In the table below, you’ll find the average UK male’s height throughout the years as given by the University of Tuebingen.
| Year | Mean Height |
| 1810 | 169.7 |
| 1850 | 165.6 |
| 1900 | 169.4 |
| 1950 | 176 |
| 1980 | 176,8 |
When to Use the Median
As previously mentioned, median is preferable when there are extreme values in the data set. The most common example of this in the real world can be found in income. Because many countries have a very tiny amount of individuals earning enormous amounts of money, the average income in a country can become highly skewed if these wealthy individuals are included.
This is why the median is preferred when reporting a centre value for income. The median is the midpoint of the value, which means that at the median there are exactly half the data below and above that point. This can be visualized in many different ways, including the bar chart below for median income given by the office for national statistics in the UK. Here, 1977 is used as the “base” year which is equal to 100.

When to Use the Mode
The mode is used in scenarios where people want to know the centre value that represents the most frequently occurring value. One of the most common uses for this in the real world is when people want to report information in terms of rank. These can include anything from the country that drink the most caffeine to the most common last name within a country.
One example can be determining the mode amongst coffee producing companies, which means that the country with the highest count of coffee production is the mode. This can be visualized in the bar chart below, which shows coffee production in thousands of 60kg sacks using data from Statistica.

Interpreting Central Tendency from Histograms
While there are endless ways to interpret a data visualization, there are a couple of general characteristics that we can glean from charts and graphs. Histograms are normally used to comment on a data set’s distribution. The characteristics of a distribution include the:
- Centre
- Spread
- Shape
While these characteristics are expanded in other sections of this guide, what we want to focus on is measures of central tendency, which deal with the “centre” characteristic. Take the following histogram.

From here, we can’t directly calculate the measures of central tendency without the actual data set. However, we can interpret the data’s centre by examining the characteristics of the histogram. For example, we can comment that the centre of the data looks to be between 97 and 109. The values are quite evenly spread around this centre, which indicates that the spread probably follows a normal distribution.
Interpreting Central Tendency from Boxplots
While boxplots and histograms display the information about a data set in different ways, what they tell us is strikingly similar. Boxplots are also used to display information about a data’s distribution. Meaning, the same characteristics can be described for a boxplot:
- Centre
- Spread
- Shape
For example, take into account the two following boxplots.
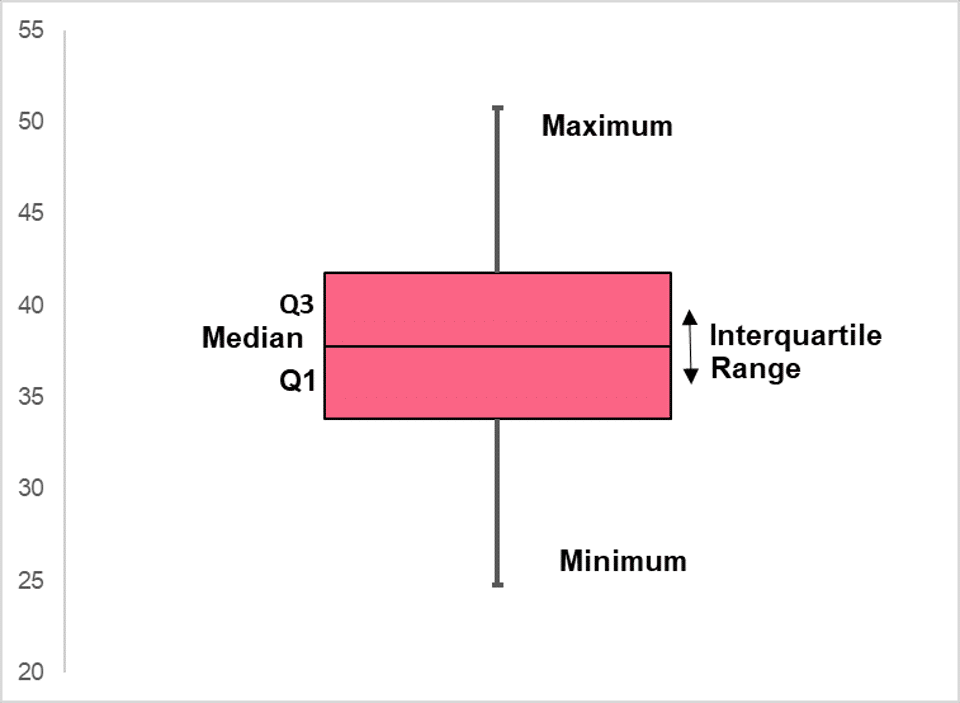
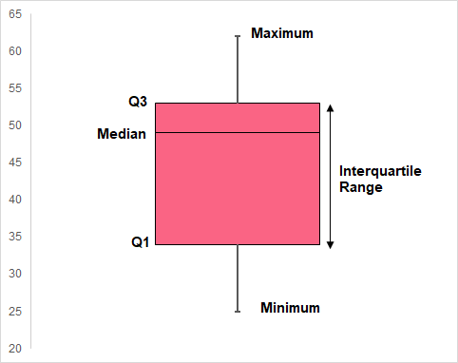
Problem 1: Which Measure of Central Tendency to Use?
Given the following histogram, which measure of central tendency do you think would be best suited to describe the data given what you’ve learned.

Solution to Problem 1
In this problem, our task was to try and decide what measure of central tendency to use. Because we have a few values that look like they could be extreme values, located at the far right, we can determine that the median or mode by be the best measures to use here.













Can you help me answer my activities