
Excat Values
Using the exact values for the sine and cosine of both 3π/4 and π/3, and the angle difference identity for cosine, find the exact value of cos(5π/12).
Answers
Okay, the key thing here is to change the fractions so they have denominators of 12, so it is easier to see the relationship:3π/4 = 9π/12 π/3 = 4π/12You can now see that cos(5π/12)=cos(9π/12 - 4π/12) and then use the trig identities to break it up then solve!
11 May 2016
Thanks so much Pri!
11 May 2016
( (sqrt(3)+1) / 2*sqrt(2) , (1/4)*sqrt(2)*(sqrt(3)-1) )
25 May 2016
There's the calculation shown explicitly :)https://i.imgsafe.org/2007d32503.jpg
16 June 2016
5Pi/12 = 3pi/4- pi/3using the formula Cos(A-B) =Cos A Cos B+Sin A Sin B Cos (5pi/12) =Cos( 3Pi/4 - pi/3) = Cos (3pi/4)Cos(pi/3) +Sin (3pi/4) Sin (pi/3) =(- sqrt2/ 2) * (1/2) + (sqrt 2 / 2 ) (sqrt 3/ 2) = ( -sqrt 2 / 4 ) +(sqrt 6 / 4) = ( -sqrt 2 +sqrt 6)/ 4 Answer
02 July 2016
Make the denominators the same:3π/4 = 9π/12 & π/3 = 4π/12 5π/12 = 9π/12 - 4π/12cos(5π/12) = cos(9π/12 - 4π/12)Use: cos(A-B) = cosAcosB + sinAsinBCos(5π/12)=cos(9π/12)cos(4π/12) + sin(9π/12)sin(4π/12) =cos(3π/4)cos(π/3) + sin(3π/4)sin(π/3) = -√2/2 x 1/2 + √2/2 x √3/2 = (√6 - √2)/4
14 January 2017
6:9~7/4^-2
12 September 2020

Add an answer
Similar questions
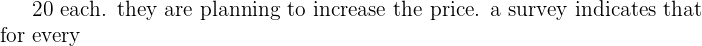 2 increase in price, there will be a drop of 60 sales a year. what should the selling price be in order to maximize the revenue?
2 increase in price, there will be a drop of 60 sales a year. what should the selling price be in order to maximize the revenue?