Chapters
Conics are curves that were studied from a very early time. A Greek mathematician Menaechmus discovered conics around the years 360-350 B.C. The Greeks defined the conics as sections of a right circular cone by planes.
A conical surface is formed by the rotation of a line, g, (also called the generatrix or generator) around another line, e, the axis, which is fixed at the point V, the vertex or apex, which forms the angle α.
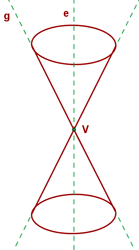
The nappes are the upper and lower portions of the conical surface which is divided by the apex. The question is what is a conical section?
A conic section is the area of intersection of a conical surface with a plane that does not pass through its apex. Depending on the relationship between the angle of a conical surface, α, and the inclination of the plane with respect to the axis, β, the conic sections will be ellipses, circles, parabola, or hyperbolas.
In simple words, conic sections are a result of the intersection of a plane and a cone. There are three types of conic sections which are parabola, hyperbola, and an ellipse. You must be wondering what about the circle? Circle is a derivative of ellipse which means that circle and ellipse were considered the same. However, new study shows that circle shouldn't be correlated with an ellipse and that is why today, circle is the fourth conical section.
When the plane is parallel to the axis of revolution (which is the y-axis and it is denoted by e in the above diagram), that means the resulting conic section will be a hyperbola. However, if the plane is parallel to the generating line (denoted by g in the above diagram), that means the resulting conic section will be a parabola. If the plane is perpendicular (intersecting at an angle of 90°) to the axis of revolution, the resulting conic section will be a circle. Last but not least, if the plane intersects a nappe at an angle (other than 90°), the resulting conic section will be an ellipse. Now you have an idea of how these conic sections were made but if you want to learn in detail then keep on reading.

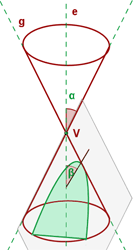
Ellipse

α is the angle from the generating line to the axis of revolution. β is the angle generated by the plane from the axis of revolution to the plane. In the above conic section, the angle α will be lesser than the angle β. The angle β will be an acute angle, here is the mathematical expression α < β < 90º. Many students get confused either the conic section is ellipse or circle? Circle and ellipse are very close to each other and the best way to identify them is to check the plane. If the plane is perpendicular to the axis of revolution that means it is a circle, otherwise it will be an ellipse. Sometimes, the β angle is so small that the plane looks perpendicular to the axis of revolution and that is why you should always measure the angle β even if you are confident that it is perpendicular or not.
Circle
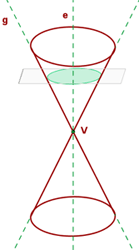
In the past, circle was usually known as ellipse since it has the same properties as an ellipse. However, new research proves that circle deserves its own importance, and today, it is the fourth conic section. If the angle β is equal to 90° that means the resulting conic section will be a circle. In simple words, if the plane is perpendicular to the axis, the conic section is a circle. Remember! Don't mix it with ellipse because circle and ellipse are two different things.
Parabola
The simplest way to find whether the conic section is a parabola or not is to look for its plane and compare it with the generating line (also known as generatrix). If both lines are parallel to each other that means it is a perfect parabola. However, the best way to define it is by measuring the angles of α and β. If both angles are equal to each other (α = β) that means the conic section is a parabola.
Hyperbola
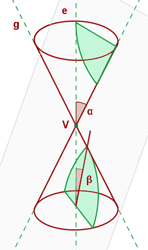
If the plane intersects two nappes of the conical surface and the angle of the generatrix, α, is greater than the inclination of the plane with respect to the axis, β, the conic section is a hyperbola. The mathematical expression is α > β. The easiest trick to find hyperbola is to look at both nappes. Hyperbola is the only conical section which cuts both nappes.
Check out various Maths tutor near me on Superprof.
Application of Conics
Of course, to this date, the idea of conics helps us to understand reality. However, it is used in many fields of study but it is mostly used in astronomy. The concept of conics helps astronomers to describe the shapes of the orbits. Furthermore, it also helps in the prediction of orbits of other planets around stars. According to the Newton's law of universal gravitation, two massive objects are in space, interacts with each other, the shape of their orbits will be similar to the conic sections. This means that they could either follow ellipse, hyperbola, or parabolic orbits according to their properties.













It’s already been in the formula, but if you reffering why the 4p was used in the formula try take chat with deepseek, it was a good gpt alternatives even better for math
Hi Enabel! Thanks for sharing this helpful advice!
It is clear and understandable .
thankyouuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu