Chapters
In the world of conic, parabola holds its importance. To completely understand parabolic trajectories, parabola equations are used. They help us to understand the parabolic path or pattern. As a matter of fact, the parabola is the base of many conics such as hyperbola, eclipse, etc. In this blog, you will learn all the equations of the parabola.

Equation of Parabola with the Vertex at Origin
Before we start to categorize equations of parabola, it is necessary for you to understand how parabola equations are developed. Let's create a parabola before we start with the derivation.
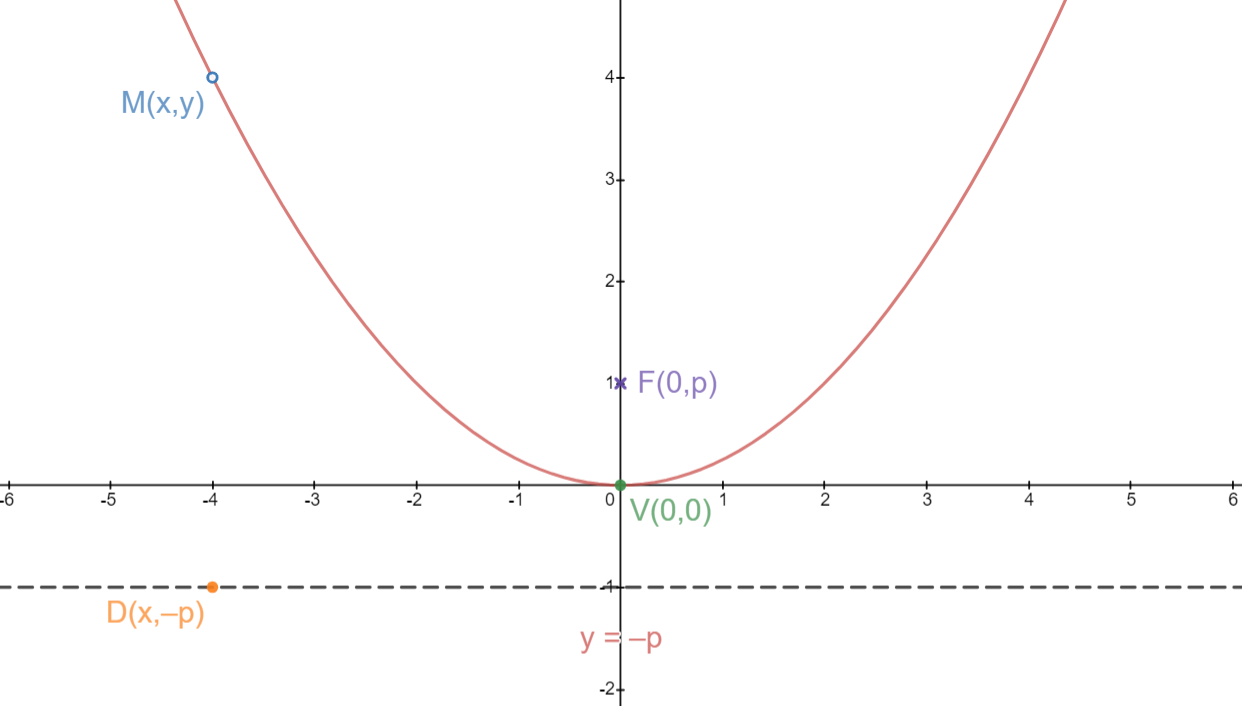
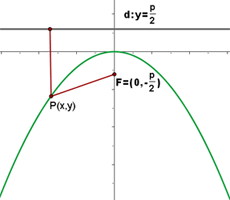
This is a parabola with vertex at the origin and the focus is on  . The directrix of this parabola is
. The directrix of this parabola is 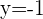 and M is just a random coordinate on the parabola. P is a variable that indicates that you can change the directrix and focus. In the above graph, p is equal to one but it can vary.
and M is just a random coordinate on the parabola. P is a variable that indicates that you can change the directrix and focus. In the above graph, p is equal to one but it can vary.
We will be using the distance formula to derive the equation of a parabola. Below is the distance formula, in case if you forgot the formula:
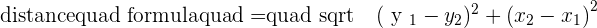
Let's find the distance of MF and MD using the distance formula.
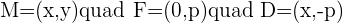

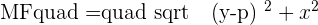
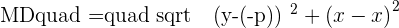
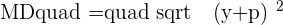
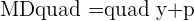
Since the distance from any random point on the parabola to the focus is equal to the distance of the same random point to the directrix, it means MD will be equal to MF.
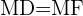
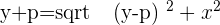

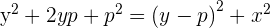


The equation of parabola whose vertex is on the origin is :
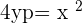
Equation of Parabola with Vertex (h,k)
Finding the parabola equation with the vertex on origin is easy, however, if the vertex isn't on the origin, it becomes a little bit complicated. The method will be the same but the equation will change. Let's create a parabola and then we will find the equation.
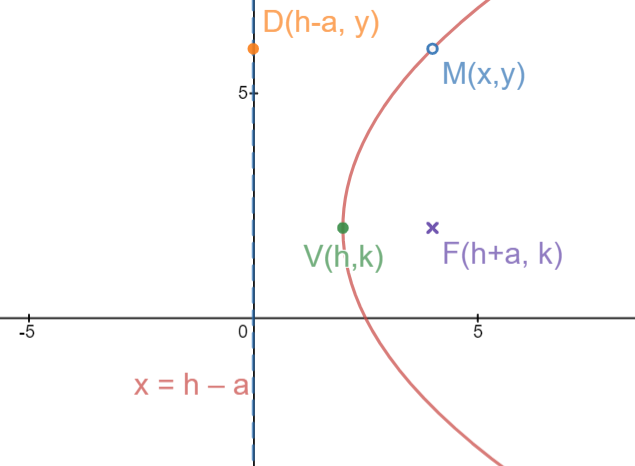
We know you are confused after looking at so many variables, in fact, there are not so many variables just 3 of them. If you can't understand the above graph then don't worry, we will also teach you how to understand it. The first thing you should be looking for the vertex. You need to understand the coordinate of vertex because it is the key to the whole puzzle. The coordinate of the vertex is represented as  in the above graph. Once you find the value of vertex, we recommend you to write down so that you don't lose the track. The next thing you should look for is the focus. To find focus, you need extra information which is denoted as "a" in the above graph. This "a" will be either given to you or you can find it by subtracting the abscissa of the vertex from the abscissa of the focus. We hope you are noting the values as we are moving forward otherwise this will confuse you a lot. Since you have found the values of a, h, and k, now the graph is easy to understand, isn't it? You can find the directrix from
in the above graph. Once you find the value of vertex, we recommend you to write down so that you don't lose the track. The next thing you should look for is the focus. To find focus, you need extra information which is denoted as "a" in the above graph. This "a" will be either given to you or you can find it by subtracting the abscissa of the vertex from the abscissa of the focus. We hope you are noting the values as we are moving forward otherwise this will confuse you a lot. Since you have found the values of a, h, and k, now the graph is easy to understand, isn't it? You can find the directrix from 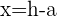 and D is just a point on the directrix.
and D is just a point on the directrix.
Now, let's focus on developing an equation of the above parabola. The method will be the same, although, new variables are introduced which means the resulting equation will be different.
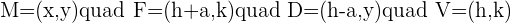
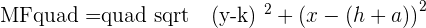
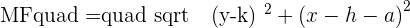

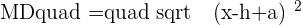
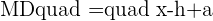
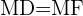
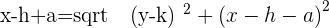
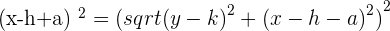
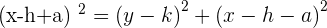
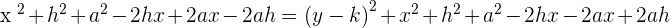
After all mathematical operations, the result will be:

Hence, the equation of a parabola with vertex (h,k) is:
Here is a question for you, what will be the equation if the value of "h" and "k" is zero and the value of a is equal to one? Let us know in the comment what will be the equation?
Horizontal Parabola
Horizontal parabola means that the directrix is parallel to the ordinate.
Parabolas with Vertex at (0, 0) and Axis on the x-Axis

The equation of the above parabola will be:
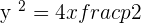
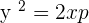


The equation of the above parabola will be:
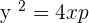


Parabola with Vertex at (a, b) and Axis Parallel to the x-Axis
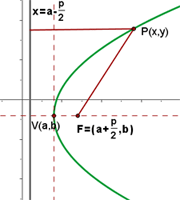
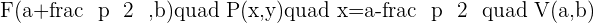
The equation of the above parabola will be:
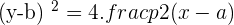

*Please don't get confused with the different variables used in this part. We are only doing this because many books use different variables so we decided to use all of them. For your information, here h is replaced a, k is replaced with b, and a is replaced with p (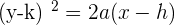 ).
).
Vertical Parabola
When the directrix of the parabola is parallel to abscissa then we call it a vertical parabola.
Parabolas with Vertex at (0, 0) and Axis on the y-Axis

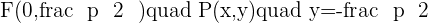
The equation of parabola will be:
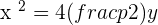
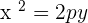

The equation of parabola will be:
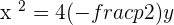
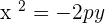
Parabola with Vertex at (a, b) and Axis Parallel to the y-Axis


The equation of parabola will be:
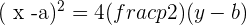
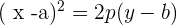
*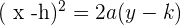
Examples
Q.1 Given the parabola 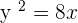 , calculate its vertex, focus, and directrix.
, calculate its vertex, focus, and directrix.
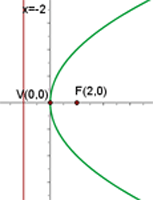
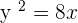

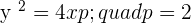
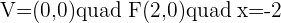
Q.2 Given the parabola  , calculate its vertex, focus, and directrix.
, calculate its vertex, focus, and directrix.
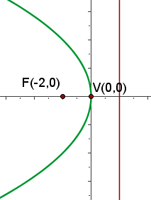


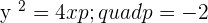
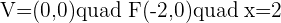
Q.3 Given the parabola  , calculate its vertex, focus, and directrix.
, calculate its vertex, focus, and directrix.
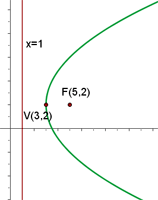

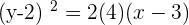

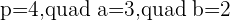

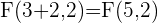


Q.4 Given the parabola 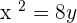 , calculate its vertex, focus, and directrix.
, calculate its vertex, focus, and directrix.
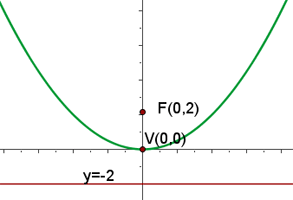
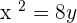
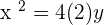
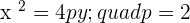
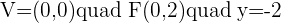
Q.5 Given the parabola 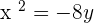 , calculate its vertex, focus, and directrix.
, calculate its vertex, focus, and directrix.
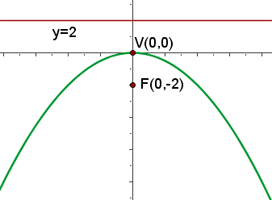
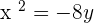
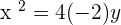

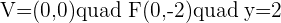
Q.6 Given the parabola  , calculate its vertex, focus, and directrix.
, calculate its vertex, focus, and directrix.
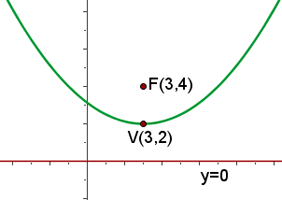

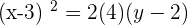
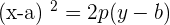
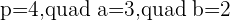

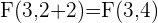














It’s already been in the formula, but if you reffering why the 4p was used in the formula try take chat with deepseek, it was a good gpt alternatives even better for math
Hi Enabel! Thanks for sharing this helpful advice!
It is clear and understandable .
thankyouuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu