Chapters

What is Hyperbola?
"A conic section that is created by an intersection of a right circular cone with a plane at such an angle that both halves of the cones intersect each other is known as a hyperbola"
In mathematics, a hyperbola is an even curve that lies in a plane. We can identify a hyperbola either by its unique geometric properties or by its solutions set of its equations. It has two parts, known as branches or connected components. These two parts are like two infinite bows and are mirror images of one another.
Remember that we can also define an ellipse as a set of points in a coordinate plane. The same applied to a hyperbola.
"A set of all points (x,y) in a plane in such a way that it has a positive difference of distances between (x,y) and the foci."
You may be thinking that this definition of the hyperbola resembles the definition of an ellipse in a coordinate plane, so what is the primary difference between two mathematical figures? Well, we define hyperbola in terms of a difference of two distances, whereas we define ellipse in terms of a sum of two distances.
Elements of Hyperbola
Like an ellipse, a hyperbola has certain elements as shown in the figure below:

Axes of Symmetry of Hyperbola
Like ellipse, a hyperbola has two axes of symmetry.
- Transverse axis: It is a line whose end points are the vertices of the hyperbola and passes through the center. The foci of the hyperbola are present on the line that has a transverse axis.
- Conjugate axis: It is the line segment whose endpoints are co-vertices of a hyperbola and is perpendicular (intersect at 90 degrees) to the transverse axis.
Center
The midpoint of both the conjugate and transverse axis is known as the center of the hyperbola. It is the point where both the axes intersect each other.
Asymptotes
From the center two asymptotes of hyperbola pass. The branches or connected components of the hyperbola approach these asymptotes as the hyperbola retreats from the center.
Center Rectangle
Its sides pass through each vertex and co-vertex of the hyperbola and it is centered at the origin. It is employed to graph a hyperbola and its asymptotes. To draw the asymptotes of the hyperbola, draw and extend the diagonals of the central rectangle.
Hyperbola Formulas
In this section, we will discuss the hyperbola standard equations and formulas.
Equations of Hyperbola Centered at the Origin
Standard equation of a hyperbola with transverse axis parallel to the x-axis
The transverse axis of a hyperbola can be parallel to the x-axis or the y-axis. The equations of both types of hyperbola vary. A hyperbola with a transverse axis parallel to the x-axis is shown below:

The standard equation of a hyperbola having its transverse axis parallel to the x-axis is given below:

Here:
- The length of the transverse axis is equal to 2a.
- The coordinates of the vertices of this hyperbola are
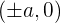
- The length of the conjugate axis is equal to 2b
- The coordinates of the co-vertices of this type of the hyperbola are

- The distance between the foci is equal to 2c, where c can be calculated by an equation

- The coordinates of the foci are
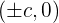
- The formula of the asymptotes of this type of hyperbola is
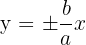
Standard equation of an hyperbola with transverse axis parallel to the y-axis
A hyperbola with a transverse axis parallel to the y -axis is shown below:
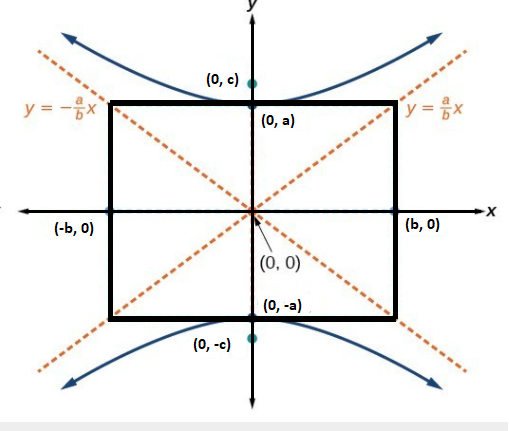
The standard equation of a hyperbola having its transverse axis parallel to the x-axis is given below:

Here:
- The length of the transverse axis is equal to 2a.
- The coordinates of the vertices of this hyperbola are

- The length of the conjugate axis is equal to 2b
- The coordinates of the co-vertices of this type of the hyperbola are
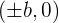
- The distance between the foci is equal to 2c, where c can be calculated by an equation

- The coordinates of the foci are
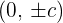
- The formula for equation of the asymptotes is
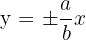
Find various Maths tutor on Superprof.
Equations of Hyperbola Not Centered at the Origin
In this section, we will see what are the equations of the hyperbola that are not centered at the origin.
Horizontal Transverse axis
The equation of a hyperbola that is not centered at the origin and has its transverse axis parallel to the x-axis is given below:
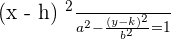
Vertical Transverse axis
The equation of a hyperbola that is not centered at the origin and has its transverse axis parallel to the y-axis is given below:

Eccentricity of the Hyperbola
The formula for finding the eccentricity of a hyperbola is given below:
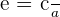 where
where 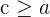 and
and 
Now, that we know the formulas of the hyperbolas, let us use the equations and formulas to solve the following examples.
Example 1
Identify vertices of the hyperbola from the following equation:

Solution
In the equation  ,
,  . Hence,
. Hence,  .
.
The vertices of the hyperbola with the horizontal transverse axis are 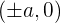 . Hence, the vertices of this equation will be:
. Hence, the vertices of this equation will be:
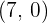 and
and 
Example 2
Identify vertices of the hyperbola from the following equation:

Solution
In the equation  ,
, 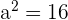 . Hence,
. Hence, 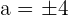 .
.
The vertices of the hyperbola with the horizontal transverse axis are 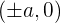 . Hence, the vertices of this equation will be:
. Hence, the vertices of this equation will be:
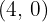 and
and 
The formula for finding asymptotes of hyperbola with the horizontal transverse axis is given below:
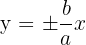
The value of b in the equation is 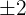 and a is equal to
and a is equal to 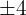 . We will substitute these values in the above formula to get the asymptotes of the hyperbola:
. We will substitute these values in the above formula to get the asymptotes of the hyperbola:
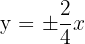
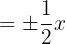
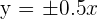
Hence, the asymptotes of the hyperbola are 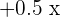 and
and 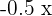 .
.
Example 3
Identify the vertices and asymptotes of the hyperbola from the following equation:
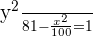
Solution
The equation above shows that the hyperbola has vertical transverse axis because the equation of the hyperbola having a vertical transverse axis is  .
.
The coordinates of the vertices of such a hyperbola are  .
.
In the equation of this example,  , hence
, hence  . Hence, the vertices of the hyperbola will be:
. Hence, the vertices of the hyperbola will be:
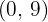 and
and 
To find the asymptotes of the hyperbola, recall the following formula for finding the asymptotes of the hyperbola with vertical transverse axis.
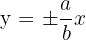
In the equation of this example,  and
and  . Substitute these values of a and b in the above formula to get the asymptotes.
. Substitute these values of a and b in the above formula to get the asymptotes.
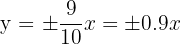
Hence, asymptotes of the hyperbola are 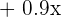 and
and  .
.













Good.