Chapters
The definition of a parabola is that it is a curve and any point on the curve is equidistant from a fixed point (which is called the focus) and a straight line (which is called directrix). Let's do a small experiment, take a piece of paper, and draw a parabola of any equation you want. You can even use desmos graph application to save your time. Mark the focus of the parabola and draw its directrix. The next thing you need to do is pick a point (on the parabola curve) and then measure the distance from the directrix line and focus. If you did everything correctly, you will see that both distances are equal to each other. That is the indication that you are working with a parabola.

Vertical Parabolas
There are two types of parabola and one of them is the vertical parabola. You might be wondering at this point what is a vertical parabola? A vertical parabola is a type of parabola that has a line of symmetry parallel to the ordinate. In other textbooks, you might read that in a vertical parabola, the directrix will be parallel to the abscissa. Parabolas don't change when they are rotated but their equation does. Below are all the equations of a vertical parabola.
Parabolas with vertex at (0, 0) and axis on the y-axis
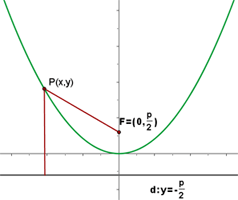
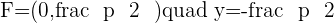
The equation of parabola will be:
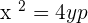
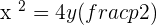

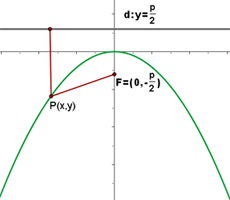
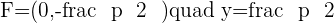
The equation of parabola will be:
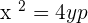

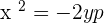
Parabola with vertex at (a, b) and axis parallel to the y-axis


The equation of parabola will be:
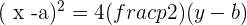
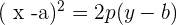
Find various Maths tutor on Superprof.
Horizontal Parabolas
Since there is a vertical parabola that means that there is a horizontal parabola as well. If you rotate the vertical parabola about 90 degrees, you will get a horizontal parabola. The indication of a horizontal parabola is that the directrix will be parallel to the ordinate. It also means that the line of symmetry of the horizontal parabola will be parallel to the abscissa. As mentioned above, when we rotate parabola, its equation also changes. Below are the equations of a horizontal parabola.
Parabolas with vertex at (0, 0) and axis on the x-axis
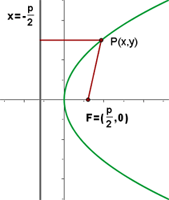
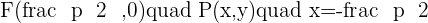
The equation of the above parabola will be:
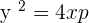
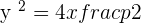
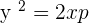


The equation of the above parabola will be:
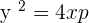


Parabola with vertex at (a, b) and axis parallel to the x-axis
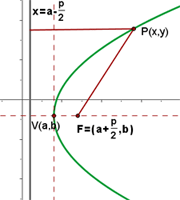
The equation of the above parabola will be:
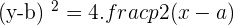

*If you want to learn the derivations of the above equations then click here.
Summarise with AI:













Good.