
Importance of Hyperbola
What is the use of maths when we don't know its importance in the real world? Everything is related to maths. For example, the colors that you are seeing right now also involves maths. The colors are, basically, a specific wavelength which has a numeric value. If you alter that numeric value, the color will change. Your eyes accept that wavelength and your brain shows you in terms of color. Think about it, if there were no wavelength in this world, the world will be black and white. You couldn't observe the beauty of the world. In the same way, hyperbola also plays an important role in our daily life.
Yes! This 2 opposite bow graph also helps in our daily life. The most use of hyperbolas is in space stations such as NASA. To launch a rocket or satellite, they use hyperbola equations to predict the path of the satellite so that it reaches the desire position. Furthermore, hyperbola equations are also used in radio stations. One of the most important radio stations which used hyperbolic towers to track things is LORAN. It helps people to track objects over a wide area. It was frequently used in world war 2. In the engineering world, hyperbolas weren't ignored. In power stations, if you observe, the cooling tower shape is hyperbolic. As a matter of fact, they are also called hyperboloid cooling towers because of the hyperbolic shape. Last but not least, the lenses in your glasses are also designed on the basis of hyperbolic function. In order to see clearly, you need to focus on it. Our eyes have a natural focus which doesn't allow us to see too close or too far. The lenses in the microscope, telescope, etc. help us to focus more closely with the help of hyperbola.
Equations of Hyperbola
There are many equations of different hyperbolas, however, they are derived from one basic equation which is 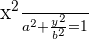 . Below are the different types of hyperbolas with their graph and equation.
. Below are the different types of hyperbolas with their graph and equation.
Hyperbolas Centered at (0, 0)
Below are all the hyperbolas and their centers are at origin (which is (0,0)).
Horizontal Transverse Axis
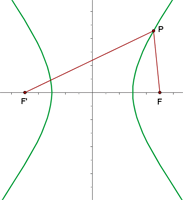
Equation of the hyperbola=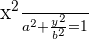
The foci of the above hyperbola are 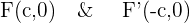 .
.
Vertical Transverse Axis

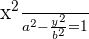 The foci of the above hyperbola are
The foci of the above hyperbola are 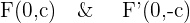 .
. Hyperbolas Centered at (x0, y0)
Horizontal Transverse Axis
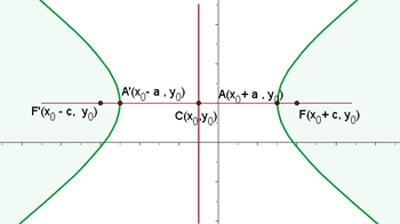
Equation of the hyperbola=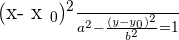
The foci of the above hyperbola are 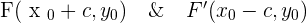 .
.
By removing the denominators, an equation is obtained in the form:
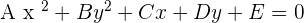
Keep in mind that A and B have opposite signs.
Vertical Transverse Axis

Equation of the hyperbola=
The foci of the above hyperbola are 
Examples
Q. Find the equation of the hyperbola of focus F = (4, 0), vertex A = (2, 0) and center C = (0, 0).
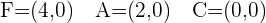
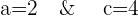
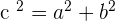
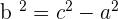

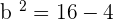
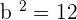
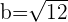
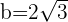
The equation of the hyperbola with center at origin is 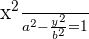 . Plugging values of a and b in the equation:
. Plugging values of a and b in the equation:

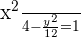
Q. Find the equation of the hyperbola of focus F = (0, 5), vertex A = (0, 3) and center C = (0, 0).
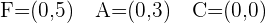

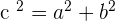
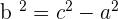

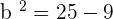
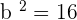
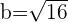

The equation of the hyperbola with center at the origin is 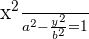 . Plugging values of a and b in the equation:
. Plugging values of a and b in the equation:


Q. Find the equation of the hyperbola of focus F = (7, 2), vertex A = (5,2) and center C = (3, 2).


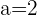
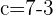
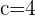
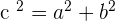
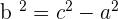

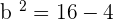
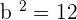
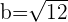
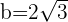
The equation of the hyperbola with center at (x0, y0) is 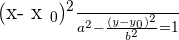
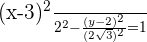

Q. Find the equation of the hyperbola of focus F = (−2, 5), vertex A = (-2, 3) and center C = (−2, −5).
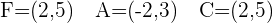

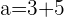
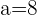
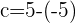
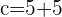
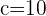
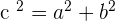
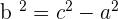
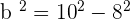
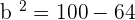
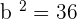

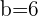
The equation of the hyperbola with center at (x0, y0) is  . Plugging values of a and b in the equation:
. Plugging values of a and b in the equation:
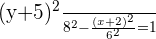

More Examples
For the following hyperbolas, determine the value of eccentricity and plot the coordinates of the center, foci, and vertices:
1. 
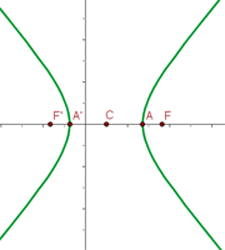
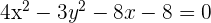
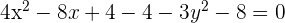

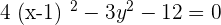
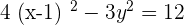
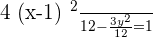
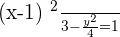
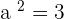

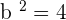
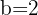
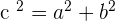

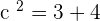

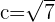


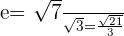



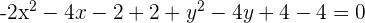
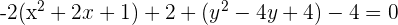
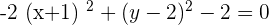
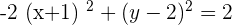

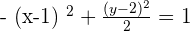

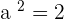
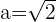

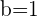
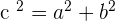
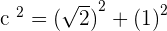

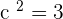
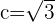
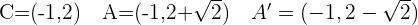
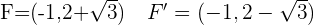
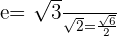













Good.