
What is Eccentricity?
In the conic chapter, we learn that there are 4 different types of shapes which are parabola, hyperbola, ellipse, and circle. They all are related to conics. When we talk about conic sections, we go back in 350 B.C when the Greek civilization discovered about different derived shapes from conic. They sliced the double cone in different ways and found 4 new shapes. If you want to learn more about conic then click here.
So, what is the difference between all these shapes? You must be thinking the structure of shape is different and you are correct, however, how you can differentiate in the world of mathematics? If you notice, they all are somewhere similar to the circle. For example, take a look at an ellipse. If you stretch a circle from the abscissa or ordinate, you will get an ellipse. Basically, an ellipse is a compressed circle. Like that, almost all the shapes are similar to a circle. You can't call them a circle since they are different shapes and possess different properties. This is where we introduce you to Eccentricity.
What is eccentricity? In many books, you will find this definition "Eccentricity measures the degree of the opening of the branches of the shapes". Let us make it easier for you. Eccentricity reveals how un-circular the curve is. Finding eccentricity is very easy but you need to understand the concept behind that.
When we find eccentricity, we always take a reference and find values relative to that reference. So, which shape we should take as a reference? The Greek mathematicians have already done the hard part. After all the calculations and intense study, they took circle as a frame of reference. This means that whenever you will find the eccentricity of any shape, you are measuring eccentricity of the shape with the reference of a circle. In simple words, you will be determining how similar your shape is to circle. If the eccentricity value is low then it means that the shape is more similar to the circle.
If we take the circle as the frame of reference then what will be the eccentric value of circle? The eccentric value of the circle is zero. It means that if the shape's eccentric value is zero, it is a perfect circle. However, if the eccentric value is, for example, 0.002 then you can't say it is a circle but if you draw this shape on a graph, it will be difficult for you to declare either the shape is a circle or ellipse. That is why eccentricity is important.
Check out various Maths tutor near me on Superprof.
What is the Eccentricity of the Hyperbola?
Since we are talking about hyperbolas here, therefore, what is the eccentric value of hyperbola? The eccentric value of hyperbola varies. In simple words, hyperbolas have a range of eccentric values. Since eccentricity defines how much is the shape curved, therefore, there is not a specific value for different hyperbolas. The reason is that we can bring minor changes in the hyperbola shape. Remember, you can bring minor changes in the hyperbola such as changing the position, the degree of the branches bending, the latus rectum, etc. That is why we have a range of values for hyperbola. It means that if the eccentric value lies in that range, you can declare that the shape is hyperbolic. The range of the eccentric values lies from 1 to infinity (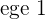 ). The formula that we use to find the eccentricity of the hyperbola is:
). The formula that we use to find the eccentricity of the hyperbola is:

Where,
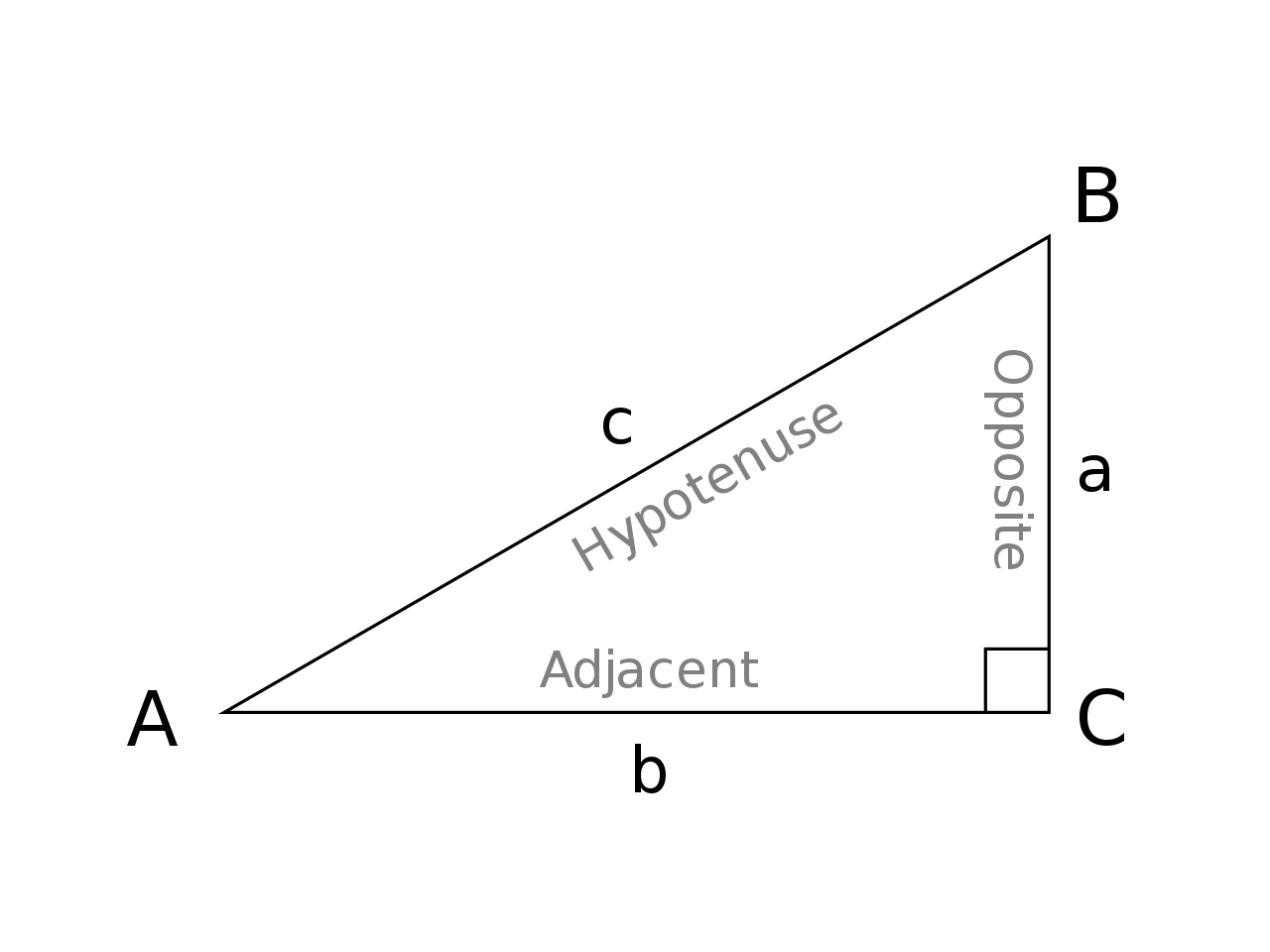
c is found with the help of the Pythagorean theorem,
and a is the distance of the semi-major axis.
We can further simplify the eccentricity formula. We will use the Pythagorean theorem and make it more simple for you to understand.
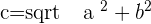
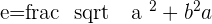
You can use any of the above formulas, both will have the same answer. It is your choice and you won't be penalized. Some of you might be thinking why hyperbolas have eccentric values more than 1? There are two answers to this question, one is in terms of maths and the last one in terms of theory, don't worry because we will tell you both reasons. Let's take a look at the values of a and c. The value of c comes from the Pythagorean theorem (which is 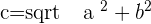 ). The value of c will always be greater (in some cases it can be equal to 1) than the value of a. That is why you will find eccentricity value will be either equal to 1 or greater than 1. In order to understand the theory, you need to have a closer look at the shape of the hyperbola. Remember, a is the semi-major axis while b is the semi-minor axis. Draw a triangle using the "a" as well as "b" coordinates and find the hypotenuse value using the Pythagorean theorem, that is your c. Since we know that the hypotenuse value is always greater than the values of adjacent (also known as base) and opposite (also known as perpendicular), therefore, we can say that c value will always be greater than the values of a and b. If we divide the value of c with the value of a, you will find that the answer will be greater or equal to 1. In conclusion, the eccentric value will always be greater or equal to 1 for hyperbolic shapes. If the eccentricity value is less than 1 then the shape will not be hyperbolic. We will discuss that later.
). The value of c will always be greater (in some cases it can be equal to 1) than the value of a. That is why you will find eccentricity value will be either equal to 1 or greater than 1. In order to understand the theory, you need to have a closer look at the shape of the hyperbola. Remember, a is the semi-major axis while b is the semi-minor axis. Draw a triangle using the "a" as well as "b" coordinates and find the hypotenuse value using the Pythagorean theorem, that is your c. Since we know that the hypotenuse value is always greater than the values of adjacent (also known as base) and opposite (also known as perpendicular), therefore, we can say that c value will always be greater than the values of a and b. If we divide the value of c with the value of a, you will find that the answer will be greater or equal to 1. In conclusion, the eccentric value will always be greater or equal to 1 for hyperbolic shapes. If the eccentricity value is less than 1 then the shape will not be hyperbolic. We will discuss that later.
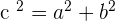

Hence, 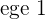
So, if we define eccentricity in terms of hyperbola then the definition will slightly be changed. Now the definition will be "Eccentricity measures the degree of the opening of the branches of the hyperbola".
Examples
Q. Find the eccentricity of the hyperbola which has a=3 and b=2.
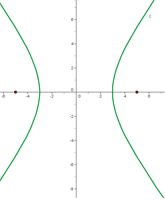
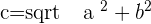
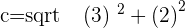

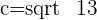

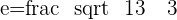
Rectangular Hyperbola
Q. Find the eccentricity of the hyperbola which has a=4 and b=4.

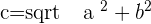
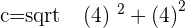

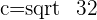


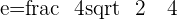

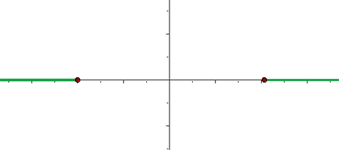
Q. Find the eccentricity of the hyperbola which has a=4 and b=0.
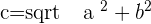
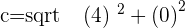
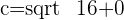
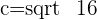
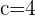

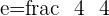
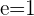













Good.