Imagine that you are playing cricket. When you hit the ball, it follows a trajectory motion. The question is what is that trajectory motion? In maths, we have named that curve (that the ball follows) as a parabola. Often, you might have heard the commentator saying that the ball is following a parabolic path, what does that mean? And how it is important for us in our daily life?
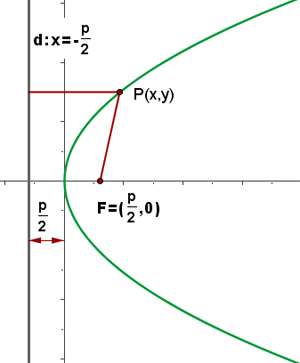
In many textbooks, you will find the same old definition which is a set of points (or locus of points) that are equidistant from a fixed point (focus) and a fixed-line (directrix line). However, there is not just one definition of a parabola. You can also define it as a U-shaped curve that has opening ends either on top, bottom, left, or right. It can also have x-intercept but it will always have a single y-intercept. Below is an image of a parabola.

Applications of Parabola
Do you know why do we study maths? To understand how things work! Math provides a basic explanation of how things work such as Earth's rotation around the sun, tidal waves, electromagnetic signals, and many more. So, how parabola helps us to understand things? The biggest use of parabola is in "Architecture and Engineering". So, if you want to pursue architecture and engineering in the near future then you must learn geometry perfectly (especially the conics section).
Parabolas are also widely used by space companies when launching a rocket such as NASA, SpaceX, etc. When the rocket launches, it follows a parabolic pattern to reduce the aerodynamic pressure. If they start to launch a rocket in a straight position, the rocket would be blown into pieces by the pressure and that is why the rockets follow a parabolic pattern.
Another real-life application of parabola is to focus light. Reflectors are made in a parabolic shape to focus light. For example, a concave lens, that lens allows spread the light and that is why many torches use a concave lens to spread the light. We have discussed a few applications of parabola here but this is not the end, there are many more applications such as satellite dish, car headlights, electron beam path through holographic film, and many more
Find various Maths tutors on Superprof.
Elements of the Parabola
There are many elements of a parabola. Of course, each element plays an important role. If one of the elements is missing that means you can't call it a parabola. Now you might understand the importance of those elements. Below are all the parts of a parabola.
Focus
A focus is a fixed point. We usually denoted focus by F. Focus will never be a point in a parabola, as a matter of fact, it will always be inside a parabola.
Directrix
Directrix is a straight line that you will always find in front of a parabola. Don't forget, it is always a straight line and it is the indication that the line is a directrix of a certain parabola. We usually represent directrix with d. In simple words, a directrix is a fixed-line.
Focal Parameter
Many students, even instructors, get confused with the focal parameter. The focal parameter is defined as the distance from the fixed point (which is the focus) to the directrix. It is mostly denoted by p.
Axis
Finding the axis of a parabola can be tricky. It helps a lot when identifying whether the parabola is horizontal or vertical. The simplest definition of an axis is that it is a line that is perpendicular (a line that cuts another line at an angle of 90 degrees) to the directrix.
Vertex
The simple definition of vertex is that it is a point that changes the direction of a parabola. Basically, it is the maximum point or the minimum point of a parabola. Sometimes it intersects with the axis and that is why in a few textbooks, the definition of the vertex changes to "a point of intersection of the parabola with its axis".













Good.