Chapters
There are a few special hyperbolas and one of them is a rectangular hyperbola. Like ellipse is a special type of circle, a rectangular hyperbola is also a special type of hyperbola. In this blog, you will learn everything about a rectangular hyperbola.

Rectangular Hyperbola
You can also call it square hyperbola as well. We will explain why you can call it square. In a few cases, when you draw asymptotes and then draw a rectangle with the help of those asymptotes, you will see that the length is equal to the breadth of that rectangle. Sounds interesting, right? Something clicking your mind? Is there any shape that has its length equal to its breath? Yes! It is a square. Now you understand why we can call it a square hyperbola as well. Another name for a rectangular hyperbola is an equilateral hyperbola.
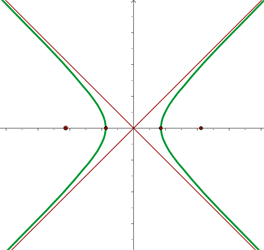
We draw a rectangle, with the help of asymptotes, to find the value of a, b, and c. In the case of rectangular hyperbola, we know that length is equal to breadth, hence, we can say that in equilateral hyperbola, the major semi-axis will be equal to the minor semi-axis. In simple words, the value of "a" will always be equal to the value of "b" in the case of a rectangular hyperbola. Let's construct the equation of a rectangular hyperbola:
Equation of hyperbola= 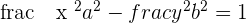
Since, 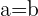 , therefore the equation will be:
, therefore the equation will be: 

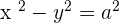
The equation of the asymptotes are 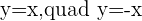
There is another method to prove the above equations. Let's import the hyperbola's asymptotes here and then apply the rectangular hyperbola rules:

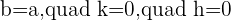


For now, let's consider  (values of h and k are equal to zero) to prove that the value of b is equal to a.
(values of h and k are equal to zero) to prove that the value of b is equal to a.

The 2 gradients of the asymptotes equation are  and
and 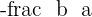 , lets put the gradient values in the above formula.
, lets put the gradient values in the above formula.

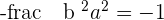
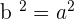
Hence, 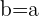
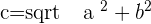
In the case of the rectangular hyperbola, it will be 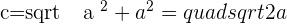

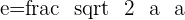
The eccentricity is 
There is another method to find the eccentricity of the equilateral hyperbola.
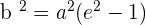
Since, 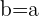
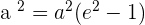

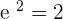
The eccentricity is 
Equation of a Rectangular Hyperbola When the Asymptotes are Rotated 45°
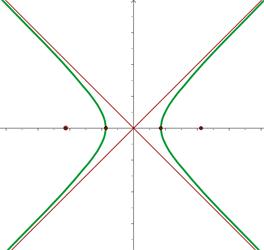
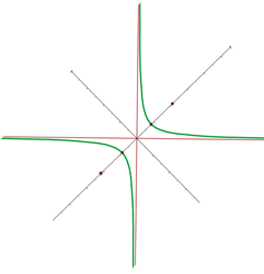
The asymptotes can be rotated at an angle of 45°. It can be clockwise 45° rotation or anticlockwise 45° rotation, however, both will have a different equation. If the hyperbola is rotated at an angle of 45°, it will lie in the second and fourth quadrant. However, if the hyperbola is rotated at an angle of -45° then the hyperbola will lie in the first and third quadrant.
If the hyperbola is rotated at an angle of 45° that means that it will have a different equation. To find the equation of equilateral hyperbola, we will need to use the concept of the polar coordinates since we are talking about angles here. First of all, convert the value of 45° to radian which is 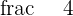 .
.

Converting to polar coordinates with 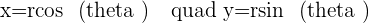 , substituting
, substituting 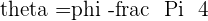 :
:

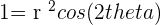
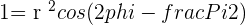
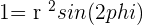

Since you know that 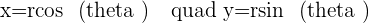 let's replace those values:
let's replace those values:
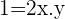

We assumed the value of a=1, however, the original formula should be:
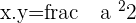
The above equation was solved for positive 45°, however, if you solve it for anticlockwise rotation45° then you should get this equation:
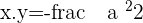

However, this isn't the finish line, it can be further simplified.
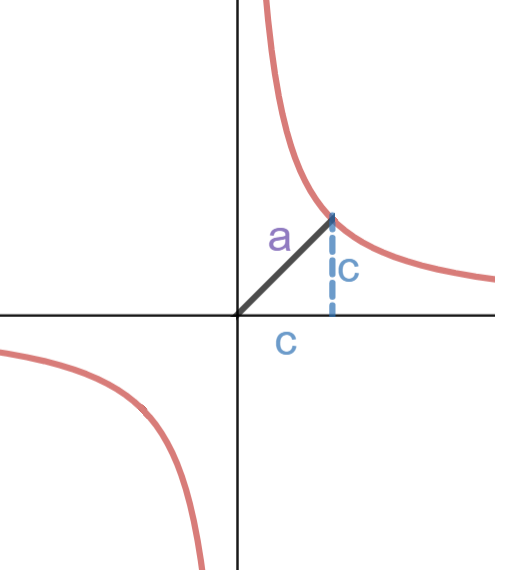
If we draw a triangle, with the help of Pythagoras theorem, we can find that:
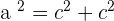

Hence, 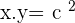
The focii of the rectangular hyperbola which is rotated 45° is 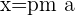 (positive a for clockwise rotation and negative a for anticlockwise rotation).
(positive a for clockwise rotation and negative a for anticlockwise rotation).
Find various Maths tutors on Superprof.
Example
Calculate the vertices and foci of a rectangular hyperbola of the equation 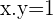 .
.
The coordinates of the vertices are on the bisector of the first and third quadrant and the first and second coordinate coincide, that is to say, x = y. Also, Point A belongs to the curve of the hyperbola.


The length of the semi-axis, a, is the distance from the origin to Vertex A.
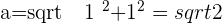

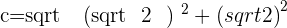
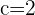
The length of the semi-axis, c, is the distance from the origin to Point C.
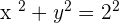
Since x=y, 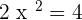
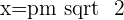














Good.