Chapters

Introduction
An ellipse is a plane curve that takes the form of a squished circle. An oval-shaped object best describes what an ellipse looks like. It surrounds two focal points in such a way that for each point in this plane curve, the sum of two distances to the focal point remains the same.
The figure below shows an ellipse with foci F (c, 0) and F'(-c, 0).
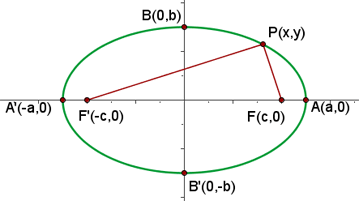
Now, that we know what an ellipse is, let us discuss what are the elements of an ellipse.
- Foci: They are also known as focus points. Foci are the fixed points of the ellipse that lie on the major axis. In the above figure F and F' represent the two foci of the ellipse.
- Major axis: You may be familiar with the diameter of the circle. A circle has only one diameter because all points on the circle are located at the fixed distance from the center. However, it is not the case with an ellipse because it is not perfectly rounded. An ellipse has two axes of symmetry: the major axis and the minor axis. Major axis is the longest diameter of an ellipse. It stretches from one side to another while passing through the center of the ellipse. In the above figure, the major axis is AA'. The length of the major axis is equal to 2a.
- Minor axis: It also stretches from one side of the ellipse to the other side while passing through the center. It is the shortest diameter of the ellipse. Both major and minor axes are the perpendicular bisectors (a segment that bisects another segment into half) of each other. In the above figure, the minor axis is represented by the points BB'. The length of the minor axis is 2b.
- Focal length: It refers to the line segment that joins two foci. In the above figure, the focal length is
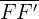 . The length of the focal length is equal to 2c.
. The length of the focal length is equal to 2c.
- Center of the Ellipse: It is the point at which the two axes (major and minor) intersect each other. We can say that it is the center of symmetry of an ellipse.
- Vertices: The points at which the ellipse intersects the axes are known as the vertices of an ellipse. In the above figure, the points A, A', B, and B' are the vertices.
- Focal radii: They refer to the line segments that join a point on the ellipse with both foci. In the above figure, the line segments
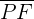 and
and 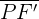 are the focal radii of the ellipse.
are the focal radii of the ellipse.
- Semi-major axis: As the name suggests, if the major axis is divided into a half, we get a new axis known as the semi-major axis. It extends from the center of the ellipse, passes through the focus point, and joins the vertex. The length of the semi-major axis is a.
- Semi-minor axis: It is half of the minor axis. Semi-major and semi-minor axes are the perpendicular bisectors of each other. The length of the semi-minor axis is equal to b.
If the lengths of the semi-major and semi-minor axis are the same, i.e. a = b, then the given figure is not an ellipse.
Ellipse Formulas
In this section, we will see what are some of the formulas of an ellipse that are useful in determining the shape and other unknown elements of the ellipse.
Relationship between the Semiaxes
We have two semiaxes, the major and minor axis. The following formula depicts the relationship between two semiaxes of the ellipse.

Eccentricity of the ellipse
Unlike a circle, an ellipse is not perfectly round, rather it is best described as an oval-shaped or squished circled figure. The eccentricity of an ellipse measures how imperfectly round an ellipse is. The formula for computing the eccentricity of an ellipse is given below:
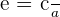 where
where 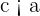
Because the foci are more closer to the center as compared to the vertices, therefore the value of e should be always less than 1. The value can be less than one only when we c is less than a. If the eccentricity is zero, then the figure is not an ellipse.
Equations of Ellipses that are centered at the origin (0,0)
Horizontal major axis
The equation of an ellipse that has the horizontal major axis is given below:

- The value of a is greater than b, i.e. a>b
- The length of the major axis is given by 2a
- The coordinates of the vertices in an xy-plane are given by
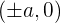
- The length of the minor axis is 2b
- The coordinates of the co-vertices in an xy-plane are

- The coordinates of the foci in an x-y plane are
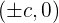 . You can find c by employing the equation taht depicts the relationship between semi-axes
. You can find c by employing the equation taht depicts the relationship between semi-axes  .
.
Vertical major axis
An equation of the ellipse that has the vertical major axis is given below:

- The value of a is greater than b, i.e. a>b
- The length of the major axis is given by 2a
- The coordinates of the vertices in an xy-plane are given by

- The length of the minor axis is 2b
- The coordinates of the co-vertices in an xy-plane are
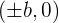
- The coordinates of the foci in an x-y plane are
 . You can find c by employing the equation that depicts the relationship between semi-axes
. You can find c by employing the equation that depicts the relationship between semi-axes  .
.
Check out various Maths tutors near me on Superprof.
Equations of the Ellipses that are not centered at the origin
Horizontal major axis
In the last section, we discussed the equations of ellipses that are centered at the origin. In this section, we will see what are the equations of ellipses that are not centered at the origin.
The following equation depicts an ellipse that is not centered at the origin and has a horizontal major axis:
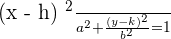
Vertical major axis
The following equation depicts an ellipse that is not centered at the origin and has a vertical major axis:
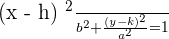
Area of an Ellipse
The formula for finding the area of an ellipse is given below:
Area of the ellipse =  . a . b
. a . b
Here, a represents the length of the semi-major axis
b represents the length of the semi-minor axis













Good.