
Introduction to Ellipse
An ellipse is an oval-shaped figure or a squished circle. It is not perfectly round like a circle. Ellipses are closed conic sections and resemble parabolas and hyperbolas. There are two axes of symmetry in an ellipse: major axis and minor axis. The major axis is the longest diameter of an ellipse and the minor axis is the shortest diameter. The major and minor axes of the ellipse perpendicularly bisect each other. The length of the major axis is equal to 2a, whereas the length of the minor axis is equal to 2b.
An ellipse also has a semi-major axis that is half of the major axis and a semi-minor axis that is half of the minor axis. The length of the semi-major axis is equal to a, whereas the length of the semi-minor axis is equal to b. The relationship between the semi-axes of the ellipse is depicted by the following formula:

The lengths of the semi-axes also help to determine the area of an ellipse which has the following formula:
Area of an ellipse = 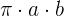
There are two focus points, i.e. foci of an ellipse. These foci are located at the major axis of an ellipse. The distance from every point on the ellipse to the two foci is constant. The distance from either focus point to the center gives us the value of c. The points at which the ellipse intersects the two axes, i.e. major and minor axes are known as vertices of the ellipse.
An ellipse can have a horizontal major axis and the vertical major axis.
An ellipse with a horizontal major axis is shown below:

The standard equation of an ellipse having a horizontal major axis is given below:
 , where a>b
, where a>b
An ellipse with a vertical major axis is shown below:
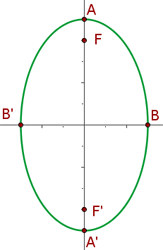
The standard equation of an ellipse having a vertical major axis is given below:
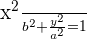 , where a>b
, where a>b
Eccentricity of an Ellipse
As we have already discussed that an ellipse is imperfectly round, unlike circular figures. We use the term eccentricity to measure an amount by which an ellipse is squished, i.e. far away from being a perfectly rounded shape. The formula for calculating the eccentricity of an ellipse is given below:
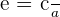
We know that the foci of an ellipse are closer to the center as compared to the vertices, therefore the value of c is always less than a. It means that the value of eccentricity will be less than 1 because we will have a smaller value in the numerator and larger value in the denominator. If you push the focus points on an ellipse gradually towards the center, then we will gradually get the figure that is nearer to being a circle. If the foci are located at the center, then it means that the value of c is 0. When the value of c will be zero, then the value of e will also become zero. When e = 0, then we say that the figure is perfectly round, i.e. it is no longer an ellipse rather it is a circle. Hence, an ellipse will always have an eccentricity value greater than 0 but less than 1. Therefore, we can say that:
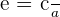 , where
, where 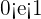
The smaller the value of e, the closer the shape of an object is to the circle. The larger the value of e, the farther away an object is from being a circle. When we say that a planet has an eccentric orbit, then we don't mean that the orbit has a strange shape, rather we mean that it is far from being a circular shape. The planetary orbits in our solar system are characterized by their eccentric shape, which means that they are far from being a circle and are of the elliptical shape.
Now we will proceed to solve some of the examples in which we will find the eccentricity of an ellipse from the given equations.
Check out various Maths tutor near me on Superprof.
Example 1
Find the eccentricity of an ellipse having the following equation:

Solution
In the above equation, the value of the denominator of the first fraction with  as a numerator is greater than the second one. Hence, the equation is of the following form:
as a numerator is greater than the second one. Hence, the equation is of the following form:

It shows that the ellipse has a horizontal major axis.
From the equation in this example, we can extract the values of  and
and 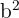 .
.
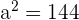 and
and 
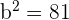 and
and 
We know that the relationship between semi-axes is given by the following formula:

Substitute the values of  and
and 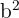 in the above equations to get the value of
in the above equations to get the value of  :
:
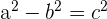

If 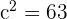 , then the value of c is equal to
, then the value of c is equal to 
The formula for computing the eccentricity of the ellipse is given below:
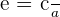
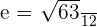

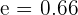
Example 2
Find the eccentricity of an ellipse having the following equation:
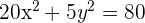
Solution
First we will convert the above equation into an equation of an ellipse. The general equation of an ellipse is given below:

We will divide the left and right hand side of the equation by 80 to make it equal to 1.

After simplifying, we will get the following equation:
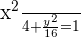
Since the denominator of  is greater than the denominator of
is greater than the denominator of  , therefore we can say that this ellipse has a vertical major axis. The equation for vertical major axis is given below:
, therefore we can say that this ellipse has a vertical major axis. The equation for vertical major axis is given below:
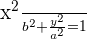 , where a>b
, where a>b
Hence, we can write the following values from the equation:
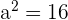 and
and 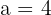
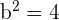 and
and 
The relationship between the semi-axes of an ellipse is given the following formula:

Putting the values of  and
and 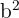 in the above equation will give us the value of
in the above equation will give us the value of 

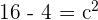


The formula for finding the eccentricity of an ellipse is given below:
Eccentricity = 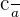
Substitute the values of c and a in the above formula to get the eccentricity value:
= 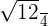
= 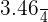
= 0.865













Good.