Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12
- Solution of exercise 13

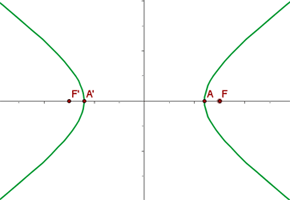
Exercise 1
Determine and plot the coordinates of the foci and vertices and calculate the eccentricity of the following hyperbolas:
1 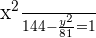
2 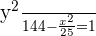
3 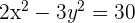
4 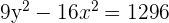
Exercise 2
Determine and plot the coordinates of the foci and vertices and calculate the eccentricity of the following hyperbolas:
1 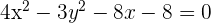
2 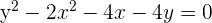
Exercise 3
Calculate the equation of the hyperbola with a transverse axis of 8 and a focal length of 10.
Exercise 4
The transverse axis of a hyperbola is 12 and the curve passes through the point P = (8, 14). Find its equation.
Exercise 5
Calculate the equation of the hyperbola centered at (0, 0) whose focal length is 34 and the distance from one focus to the closest vertex is 2.
Exercise 6
Determine the equation of the hyperbola centered at (0, 0) that passes through the points: 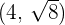 and
and  . .
. .
Exercise 7
Determine the equation of the hyperbola centered at (0, 0) that passes through the point  and whose eccentricity is
and whose eccentricity is 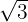 .
.
Exercise 8
Determine the equation of the hyperbola centered at (0, 0) knowing that one focus is 2 units from one vertex and 50 from the other.
Exercise 9
Determine the coordinates of the point(s) of intersection between the line x + y − 1 = 0 and the hyperbola  .
.
Exercise 10
A rectangular hyperbola passes through the point 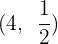 . Find its equation and determine the coordinates of the vertices and foci.
. Find its equation and determine the coordinates of the vertices and foci.
Exercise 11
The transverse axis of a hyperbola is 12 and the eccentricity is  . Calculate the equation of this hyperbola.
. Calculate the equation of this hyperbola.
Exercise 12
Calculate the equation of a rectangular hyperbola knowing that its focal length is  .
.
Exercise 13
The length of the conjugate axis of a hyperbola is 8 and the equations of the asymptotes are:  . . Calculate the equation of the hyperbola, its foci and vertices.
. . Calculate the equation of the hyperbola, its foci and vertices.
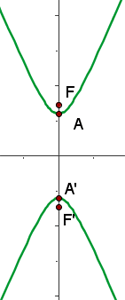
Solution of exercise 1
Determine and plot the coordinates of the foci and vertices and calculate the eccentricity of the following hyperbolas:
1 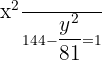
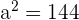

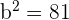

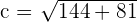
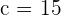
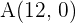

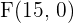
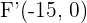

2 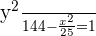
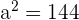


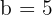
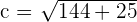
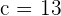

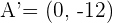
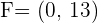

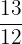
3 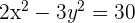
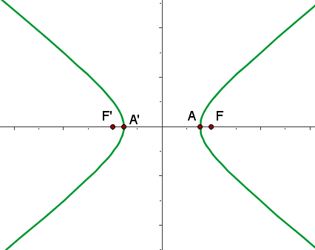
Divide by 30:

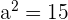
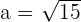

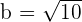


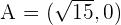
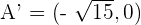
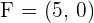


4 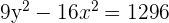

Divide by 1296:
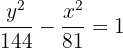
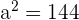

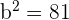

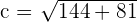
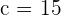
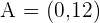
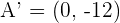
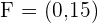

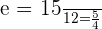
Solution of exercise 2
Determine and plot the coordinates of the foci and vertices and calculate the eccentricity of the following hyperbolas:
1 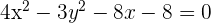
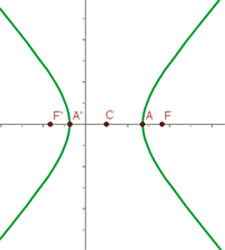
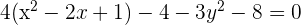
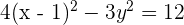
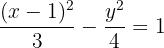


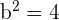




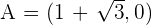
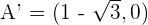
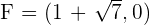
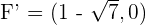
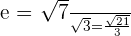
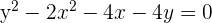

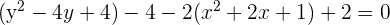

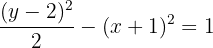
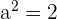
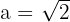
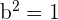


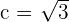
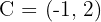

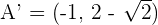
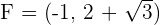
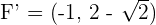
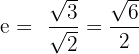
Solution of exercise 3
Calculate the equation of the hyperbola with a transverse axis of 8 and a focal length of 10.
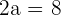
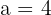
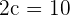



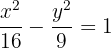
Solution of exercise 4
The transverse axis of a hyperbola is 12 and the curve passes through the point P = (8, 14). Find its equation.
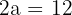


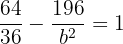
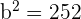
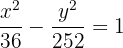
Solution of exercise 5
Calculate the equation of the hyperbola centered at (0, 0) whose focal length is 34 and the distance from one focus to the closest vertex is 2.
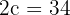
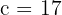
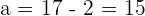
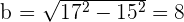
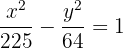
Solution of exercise 6
Determine the equation of the hyperbola centered at (0, 0) that passes through the points: 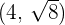 and
and  .
.
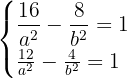
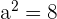
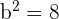
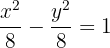
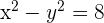
Solution of exercise 7
Determine the equation of the hyperbola centered at (0, 0) that passes through the point  and whose eccentricity is
and whose eccentricity is 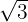 .
.
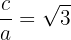
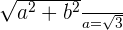
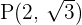
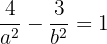
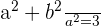
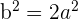
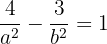
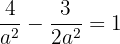


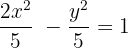
Solution of exercise 8
Determine the equation of the hyperbola centered at (0, 0) knowing that one focus is 2 units from one vertex and 50 from the other.
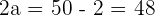
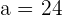
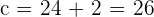
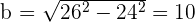
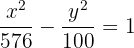
Solution of exercise 9
Determine the coordinates of the point(s) of intersection between the line x + y − 1 = 0 and the hyperbola x² - 2y²= 1.

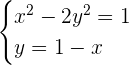

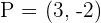
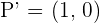
Solution of exercise 10
A rectangular hyperbola passes through the point (4, 1/2). Find its equation and determine the coordinates of the vertices and foci.
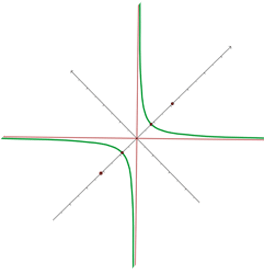
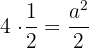

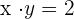
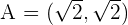
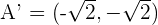

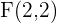
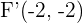
Solution of exercise 11
The transverse axis of a hyperbola is 12 and the eccentricity is 4/3. Calculate the equation of this hyperbola.
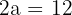

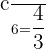
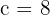
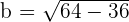

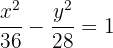
Solution of exercise 12
Calculate the equation of a rectangular hyperbola knowing that its focal length is  /
/ 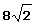
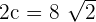




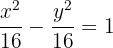

Find various Maths tutor on Superprof.
Solution of exercise 13
The length of the conjugate axis of a hyperbola is 8 and the equations of the asymptotes are: 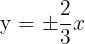 . Calculate the equation of the hyperbola, its foci and vertices.
. Calculate the equation of the hyperbola, its foci and vertices.


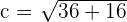

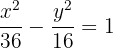

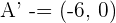

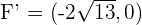













It’s already been in the formula, but if you reffering why the 4p was used in the formula try take chat with deepseek, it was a good gpt alternatives even better for math
Hi Enabel! Thanks for sharing this helpful advice!
It is clear and understandable .
thankyouuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu