Chapters
In mathematics, an intersection of two or more objects means a point at which these objects intersect or touch each other. A line segment is a straight line with two fixed endpoints, whereas a circle is a figure in which all points are located at a fixed distance from the centre of the circle. In this article, we will discuss the intersection of a line and a circle. So, let us get started.

Ways in Which a Line Can Intersect a Circle
A line can intersect a circle in the following three ways:
- If a line intersects or cuts through the circle, then we will get two points of intersection as shown in Figure 1.1. below.

You can see that in the above figure, the red line intersects the circle at two points. In this case, 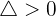 .
.
2. If a tangent line is drawn to the circle, then we will have only one point of intersection as shown in the figure below:

You can see that the red line is tangent to the green circle as it cuts the circle at a single point only. In this case, 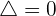 .
.
3. If a line does not touch the circle at all, then there will be no point of intersection as shown in the figure below.

You can see that the red line does not touch the circle at all. Hence, we can say that there is no point of intersection. In this case,  .
.
Find more Maths tutor here on Superprof.
Steps for Finding a Point of Intersection of a Line and Circle
If we are given a linear equation of a line and a general equation of a circle, we can easily find whether the line intersects the given circle or not. To do so, we should follow the following steps:
- Substitute the linear equation into the equation of a circle. Often linear equations are given in terms of y. We will substitute the y-values of the equation of a circle with y value of the linear equation
- Simplify the equation to get a quadratic equation.
- Factorise the quadratic equation by expanding the middle term.
- Find roots, i.e the values of x. Substitute the values of x in the linear equation to get the corresponding y-values.
Note: You can also employ the quadratic formula to calculate the roots of the equation.
Now, we will proceed to solve some of the examples of circle-line intersection, which will make the above steps clearer.
Circle-Line Intersection Problems and Solutions
Show that the line y = x + 4 intersects the circle 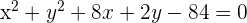 , and also determine the point of intersection.
, and also determine the point of intersection.
We are given a linear equation 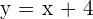 .
.
The equation of a circle = 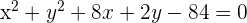
Substitute 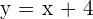 in the equation of the circle
in the equation of the circle 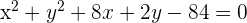 .
.
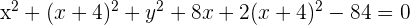
We know that 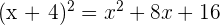 :
:
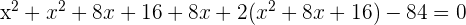

Combine the like terms together:
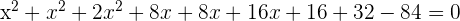

Divide the entire equation by a constant 4 to simplify it:
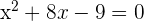
Factorize the above quadratic equation by expanding the middle term:
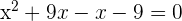
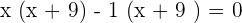

 or
or 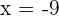
Substitute the values of x, that are 1 and - 9 in the linear equation 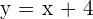 to get the value of y.
to get the value of y.
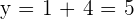

This shows that the line 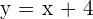 intersects the circle
intersects the circle 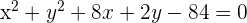 at the points (1, 5 ) and ( -9 , -5).
at the points (1, 5 ) and ( -9 , -5).
Show that the line 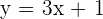 intersects the circle
intersects the circle  , and also determine the point of intersection.
, and also determine the point of intersection.
We are given a linear equation 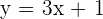 .
.
The equation of a circle = 
Substitute 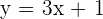 in the equation of the circle
in the equation of the circle  .
.
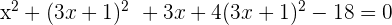
We know that 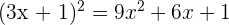 :
:


Combine the like terms together:
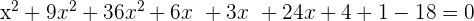
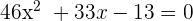
Factorize the above quadratic equation by expanding the middle term:
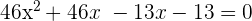


 or
or 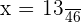
Substitute the values of x, that are -1 and 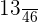 in the linear equation
in the linear equation 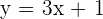 to get the value of y.
to get the value of y.
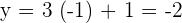
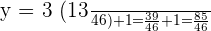
Hence, the line  intersects the circle
intersects the circle  at the points
at the points 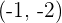 and
and 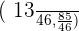 .
.
Determine the points of intersection of the line  and the circle
and the circle  .
.
We are given a linear equation  .
.
The equation of a circle:
 .
.
Substitute  in the equation of the circle
in the equation of the circle  .
.




Divide the equation by 2 to simplify it:
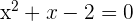
Factorize the above equation to get the roots of the equation:
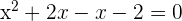
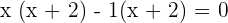

 or
or 
Substitute the values of x in the equation  to get the y-coordinates of the line:
to get the y-coordinates of the line:
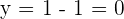

Hence, the line  intersects the circle
intersects the circle  at points (1, 0) and (- 2, -3).
at points (1, 0) and (- 2, -3).
Show that the line 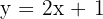 intersects the circle
intersects the circle 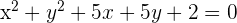 , and also determine the point of intersection.
, and also determine the point of intersection.
We are given a linear equation 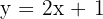 .
.
The equation of a circle:
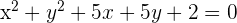
Substitute 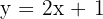 in the equation of the circle
in the equation of the circle 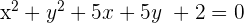 .
.
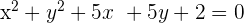

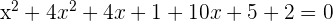

Factorize the above equation to get the roots of the equation:


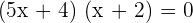
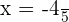 or
or 
Substitute the values of x in the equation 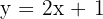 to get the y-coordinates of the line:
to get the y-coordinates of the line:
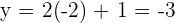
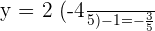
Hence, the line 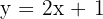 intersects the circle
intersects the circle  at points
at points 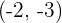 and
and 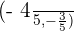 .
.
Show that the line 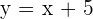 is tangent to the circle
is tangent to the circle 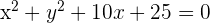 , and also determine the point of tangency.
, and also determine the point of tangency.
Given the equation of the line = 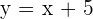
Equation of the circle = 
Substitute 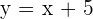 into the equation of the circle
into the equation of the circle 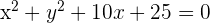 to get the x and y intercepts of the tangent line:
to get the x and y intercepts of the tangent line:
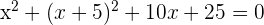

Add the like terms together to get the following expression:

Divide the equation by 2 to simplify it:
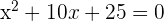
Factorize the quadratic equation to find roots:


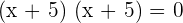

Substitute  in the equation of a line
in the equation of a line 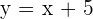 to get the value of y coordinate:
to get the value of y coordinate:
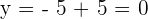
Hence, the line 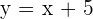 intersects the circle
intersects the circle 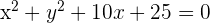 at a single point only. We know that a line tangent to the circle intersects it at a single point only. Therefore, we can say that the line in this example is tangent to the circle. The tangent point in a coordinate plane is
at a single point only. We know that a line tangent to the circle intersects it at a single point only. Therefore, we can say that the line in this example is tangent to the circle. The tangent point in a coordinate plane is  .
.
Check out affordable Maths tuition on Superprof.













Good.