Chapters
The definition of a circle is given below:
"All set of points in a circle are at the fixed distance from its center"
In this article, we will see the formula to find the center and radius of the circle. We will also see how to use completing the square method to convert the equation into a center-radius form. So, let us get started.

Formula for Finding the Center and Radius of a Circle
The equation of the circle in center-radius form which has the center at the point (h,k) and radius 'r' is given below:

The above equation of the circle can be used to find the center of the circle and its radius.
The equation of the circle having the origin as its center is given below:

Let us find the center and radius of the circle using the above formulas in the following examples.
Example 1
Find the center and radius of the circle whose equation is given below:
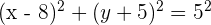
Solution
We know that the formula for the equation of the circle is:

The center of the circle is at the point (h,k) and r is the radius of the circle. We are given the following equation:
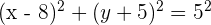
It shows that:

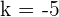
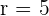
Hence, the center of the circle is at the point (8, -5) and the radius is 5.
Example 2
Find the center and radius of the circle whose equation is given below:
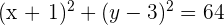
Solution
We know that the formula for the equation of the circle is:

The center of the circle is at the point (h,k) and r is the radius of the circle. We are given the following equation:
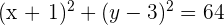
It shows that:


Since  , therefore
, therefore 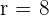 .
.
Hence, the center of the circle is at the point (-1,3) and the radius is 8.
Example 3
Write the equation of the circle whose center is at the point (3,9) and the diameter is 14.
Solution
In this example, we are given the point (h,k) of the circle and diameter. We know that the center-radius formula of the circle is:

Substitute h = 3 and k = 9 in the above equation:

The next point is to substitute the radius in the equation of the circle. We are not given the radius in this example. Instead, we are given the diameter of the circle. We know that the diameter. If the diameter of the circle is 14, then its radius must be 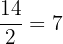 . Substituting the radius in the equation will complete the equation of the circle:
. Substituting the radius in the equation will complete the equation of the circle:

Example 4
Write the equation of the circle whose center is at the point (-4, 7) and the circumference is 62.8 cm.
Solution
In this example, we are given the point (h,k) of the circle and diameter. We know that the center-radius formula of the circle is:

Substitute 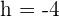 and
and 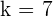 in the above equation like this:
in the above equation like this:

We need to also substitute the radius of the circle in the above equation to complete it. However, we are not given the radius of the circle in this example. Instead, we are given the value of the circumference of the circle. If we are given the circumference of the circle, we can still find its radius. The formula of circumference of the circle is given below:
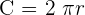
Substitute the value of the circumference = 62.8 and 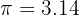 in the above equation:
in the above equation:
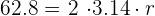
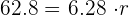
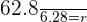
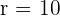
Substitute this value of r in the equation like this:
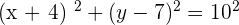
Check out affordable Maths tuition on Superprof.
Completing the Square Method
We employ completing the square method to turn a quadratic equation into a sum of a squared binomial (a polynomial having two terms) like this:
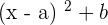
You can be given the equation of the circle in the following format:

To find the radius and center of the circle, you need to convert the above equation to the center-radius form by following a procedure known as "completing the square".
Example 1
The equation of the circle is given below. Find its radius and center.
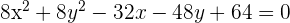
Solution
The equation of the circle in this example is not given in the form  .Hence, we need to convert it into this form by following a method known as completing the square. To do so, follow the steps below:
.Hence, we need to convert it into this form by following a method known as completing the square. To do so, follow the steps below:
Step 1
You can see that all the terms in the above equation are multiples of 8. Hence, we will divide the entire equation by 8 to simplify it and shift the constant to the right-hand side of the equation like this:
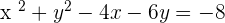
Step 2
In this step, we will write the terms having the same variable together like this:

Step 3
This is the most important step. In this step, we will use the completing the square method to convert the above equation into the following form:

To use the method, we need to take the coefficient of x, divide it by 2, square it, and add it to both sides of the equation. We will apply the same procedure using the coefficient of y.
In this example, the coefficient of x is 4. First, we will divide it by 2 to get 2. Now, we will add the square of 2 to both sides of the equation. Similarly, the coefficient of y is 6. First, we will divide 6 by 2 to get 3, and take the square of 3 and add it to both sides of the equation.

We know that 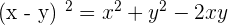 . We will use this formula to write the above equation in this form:
. We will use this formula to write the above equation in this form:
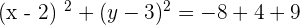

Step 4
Now, we can easily spot the center of the equation (h,k) and radius from the equation  .
.
Here, 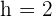 ,
,  and
and 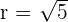 .
.
Example 2
The equation of the circle is given below. Find its radius and center.
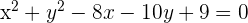
Solution
We will follow the following steps to write the above equation in this form:
 .
.
We do not need to simplify the equation given in this example because all the terms are not the multiples of a single constant.
Step 1
In this step, we will write the terms having the same variable together like this:

Step 2
This is the most important step. In this step, we will use the completing the square method to convert the above equation into the following form:

To use the method, we need to take the coefficient of x, divide it by 2, square it, and add it to both sides of the equation. We will apply the same procedure using the coefficient of y.
In this example, the coefficient of x is 8. First we will divide it by 2 to get 4. Now, we will add the square of 4 to both sides of the equation. Similarly, the coefficient of y is 10. First, we will divide 10 by 2 to get 5, and take the square of 5 and add it to both sides of the equation.
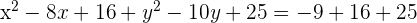
We know that 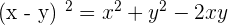 . We will use this formula to write the above equation in this form:
. We will use this formula to write the above equation in this form:

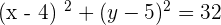
Step 3
Now, we can easily spot the center of the equation (h,k) and radius from the equation 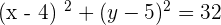 .
.
Here,  ,
, 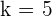 and
and  .
.
Find more Maths tutor here on Superprof.













Good.