
What is an Ellipse?
You are familiar with the circular shapes. All points in a circle are located at a definite distance from the center. A circle has no edges or vertices. An ellipse is an oval-shaped or squished circle. A standard ellipse looks like this:

Each ellipse has two axes of symmetry, the major axis, and the minor axis. The major axis is the longest axis and the minor axis refers to the shortest axis. Vertex or vertices (plural) of the ellipse are located at the endpoints of the major axis. The co-vertex of the ellipse refers to each endpoint of the shorter i.e. minor axis.
The midpoint of the larger and smaller axis is the center of the ellipse. Major and minor axes of the ellipse are perpendicular to each other at the center of the ellipse. The foci or the focus points of the ellipse are present on the major axis. The aggregate to the distance from the foci to any point of the ellipse is always greater than the distance between the two foci. The foci of the ellipse in figure 1.1 are F and F'. An ellipse is also defined in terms of foci like this:
It is the set of all points (x,y) in such a way that the aggregate of the distances from the points (x,y) to the foci or focus points are the same.
Equation of an Ellipse
The standard form of equations is important as it helps us to interpret the primary features of the graphs. You may have worked with the standard form of linear, quadratic, exponential, or logarithmic functions in the past. Analyzing the standard form of the equations help us to gauge how their geometric and algebraic representations of the are related to each other.
Before proceeding to the equation, you must know the fundamental features of the ellipse such as its center, vertices, foci, co-vertices, and the major and minor axes. We can interpret and recognize all these key features of the ellipse by looking at its standard equation.
Horizontal Major Axis


Remember that in the above equation:
- a is greater than b, i.e. a>b
- The major axis's length is 2a.
- The coordinates of the vertices in an x-plane are
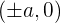 .
. - The length of the minor axis is equal to 2b
- The coordinates of the co-vertices in an x-y plane are

- The coordinates of the foci in an x-y plane are
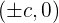 . You can find c using the equation
. You can find c using the equation  .
.
You can interpret all the above listed key features of an ellipse by just looking at its equation.
Vertical Major Axis
In this section, we will discuss the equation of an ellipse when the major axis is parallel to the y-axis, i.e it is vertical. Figure 1.3 depicts how an ellipse looks like in this situation:
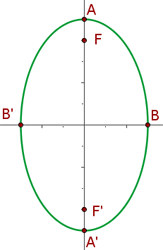
The standard form of its equation of an ellipse when the major axis is vertical is given below:
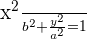
Remember that in the above equation:
- a is greater than b, i.e. a>b
- The major axis's length is 2a.
- The coordinates of the vertices in a xy-plane are
 .
. - The length of the minor axis is equal to 2b
- The coordinates of the co-vertices in an x-y plane are
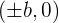
- The coordinates of the foci in an x-y plane are
 . You can find c using the equation
. You can find c using the equation  .
.
Just like the ellipse with a horizontal major axis, you can interpret all these key features of the ellipse by looking at its equation.
Check out various Maths tutor near me on Superprof.
Equation of the Ellipse if Vertices and Foci are not centered at the Origin
So far, we have discussed the equations of the ellipse when its vertices and foci are centered at the origin. In this section, we will discuss how the equation varies if these two key features are not centered at the origin. If the vertices and foci are not centered at the origin and the major axis is horizontal, then the equation of such an ellipse is given below:
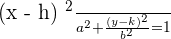
If the vertices and foci are not centered at the origin and the major axis is vertical, then the equation of such as ellipse is given below:
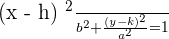
Eccentricity of the Ellipse
Unlike a circle, an ellipse is not perfectly round. An ellipse eccentricity means how squished or far away an ellipse is from a circle. The equation to determine the eccentricity of an ellipse is given below:
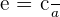
Examples
Now, we will use the equations of the ellipse to solve some examples.
Example 1
Find the elements and the equation of the ellipse when foci are F' = (−5, 0), F = (5, 0) and the length of the major axis is equal to 14.
Solution
Find a
Since the length of the major axis of the ellipse = 2a, hence a = 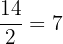 .
.
Find c
The distance between the two foci = 2c. The coordinates of two foci are (−5, 0) and (5, 0). The distance between the foci 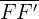 is equal to 10. Hence, c = 5.
is equal to 10. Hence, c = 5.
Find b
We know that  .
.
Put the values of c and a in the above equation to determine the value of b

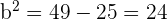
Write the Equation
Now, we will substitute  and
and 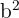 in the equation below to determine the equation of the ellipse:
in the equation below to determine the equation of the ellipse:

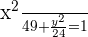
Eccentricity of the Ellipse
Since, we know the values of c and a, therefore we can find the eccentricity of the ellipse by substituting these values in the equation below:
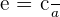
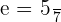
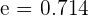
Example 2
Given the equation of an ellipse 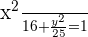 , find the eccentricity, and coordinates of the vertices and foci.
, find the eccentricity, and coordinates of the vertices and foci.
Solution
We know that in the equation of the ellipse, a is always greater than b. The equation of the ellipse in this example is 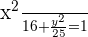 , which shows that
, which shows that  should be 25. If
should be 25. If  is 25, then the value of a should be 5.
is 25, then the value of a should be 5.
The equation in this example is of the following form, which shows that the major axis of the ellipse is vertical.
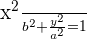
Coordinates of the vertices
If the ellipse has vertical major axis, then the coordinates of the vertices are  . The value of a is 5, so the coordinates of the vertices are:
. The value of a is 5, so the coordinates of the vertices are:

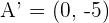
Coordinates of the foci
The coordinates of the foci of the ellipse with vertical major axis are  . From the equation, we know that the value of
. From the equation, we know that the value of  , hence b is equal to 4. Put the value of a = 5 and b =4 in the equation below:
, hence b is equal to 4. Put the value of a = 5 and b =4 in the equation below:

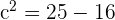
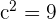

Put the value of c =3 in the  . Hence, the coordinates of the foci are:
. Hence, the coordinates of the foci are:
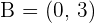
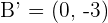
Eccentricity
Put the value of c = 3 and a = 5 in the below equation to get the eccentricity of the ellipse:
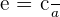
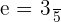














Good.