Chapters
A parabola is one of the most important and fascinating curves in mathematics. It appears in physics, engineering, architecture, and even everyday life — from the path of a thrown ball, to the shape of satellite dishes and car headlights.
In coordinate geometry, the parabola belongs to the family of conic sections — curves formed when a plane cuts through a cone. Mathematically, a parabola is defined as the set of all points that are equidistant from a fixed point (the focus) and a fixed line (the directrix).
Vertex (V) — the turning point of the parabola.
Focus (F) — a fixed point inside the curve.
Directrix (D) — a fixed line outside the curve, opposite the focus.
Axis of symmetry: The line passing through the vertex and the focus.

Deriving the Standard Equation
Let’s consider the simplest case — a parabola whose vertex is at the origin (0, 0) and which opens upward.
- Focus: (0,p)
- Directrix: y=−p
- Axis of symmetry: y-axis
For any point P(x,y) on the parabola:
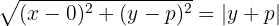
Squaring both sides and simplifying gives:
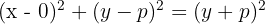
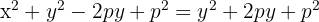
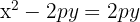
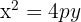
This is the standard equation of a vertical parabola (opening upward if p>0, downward if p<0).
Similarly, for a horizontal parabola (opening right or left):
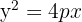
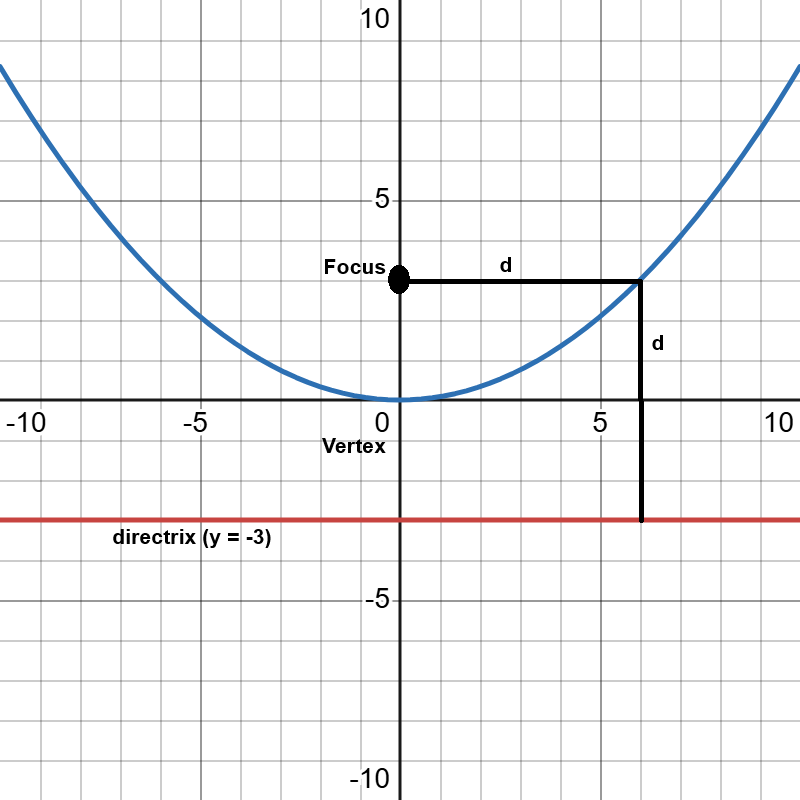
Below is a diagram showing a simply parabola opening upwards, with vertex at (0,0), focus at (0,3), directrix at y=-3 and the y-axis as the axis of symmetry:
Variations to the Standard Equation
If we shift the parabola so that its vertex is no longer at (0, 0), but at (h, k), then every point on the parabola must now be measured relative to that vertex. This means:
- Instead of x, we use (x−h)
- Instead of y, we use (y−k)
This gives us the vertex form of the parabola.
For a vertical parabola (axis of symmetry parallel to the y-axis):
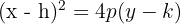
For a horizontal parabola (axis of symmetry parallel to the x-axis):
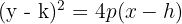
- (h, k) → coordinates of the vertex
- p → distance from the vertex to the focus
- The directrix is located the same distance p on the opposite side of the vertex
Practice Questions and Answers
Find the equation of the parabola with directrix x = −3 and focus (3, 0).
Vertex is midway between the focus and directrix:
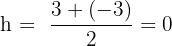
Vertex = (0, 0)
Since the parabola opens rightward, its equation is of the form:
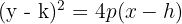
Substituting vertex (0, 0) and p = 3:
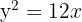
Find the equation of the parabola with directrix y = −5 and focus (0, 5).
Vertex is halfway between focus and directrix:
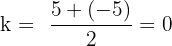
Vertex = (0, 0), parabola opens upward.
Equation form:
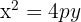
Substitute p = 5:

Find the equation and directrix of the parabola with focus (2, 0) and vertex (0, 0).
Opens to the right, standard form:
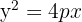
Since p = 2:

Directrix: x = −2
Find the equation of the parabola with directrix y = 0 and focus (2, 4).
Vertex lies halfway between focus and directrix vertically:
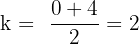
Vertex = (2, 2), p = 2, opens upward.
Equation form:
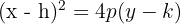
Substitute (h, k) = (2, 2):
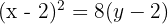
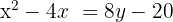
Find the equation of the parabola with focus (0,−4) and directrix y=2y.
Vertex is midway between focus and directrix (vertical axis of symmetry):
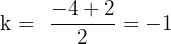
Vertex = (0, −1)
Distance p from vertex to focus (negative → opens downward):
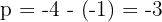
Use the vertical vertex form:
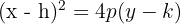
Substitute h=0, k=−1, p=−3:
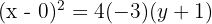
Simplify:
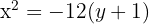












Good.