
The best Maths tutors available
Slope Formulas
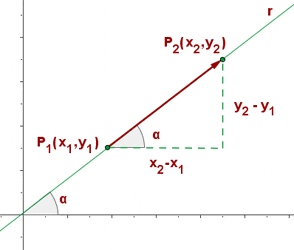
Slope of two given points
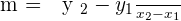
Slope of the given angle

Slope of a given vector of the line
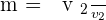
Slope of the given equation
Compare the equation with 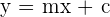 , where m is the gradient of that specific line.
, where m is the gradient of that specific line.
Line Formulas
Distance between two points


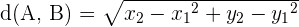
Vector equation

Parametric form

Point slope

General form
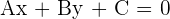
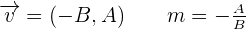
Slope-Intercept form
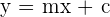 , where c is the y-intercept
, where c is the y-intercept
Intercept form
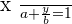
Two-points form

Vertical and horizontal lines
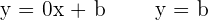

Parallel lines


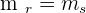
Perpendicular lines

Angle between two lines
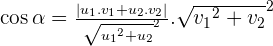
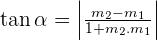
Distance from a point to a line

Perpendicular bisector

Angle bisector
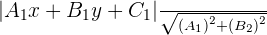
Line in Space
Vector form

Parametric form
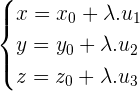
Cartesian equations
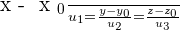
Intercept form
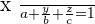
Plane Formulas
Vectorial Equation of the plane
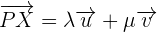

Parametric equations of the plane
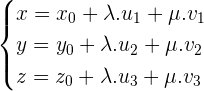
Cartesian equation of the plane

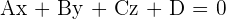
Intercept form
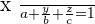

Conic Sections Formulas
Circle Equations
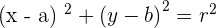
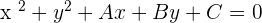
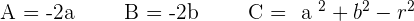

Circle with the origin at its center

Ellipse


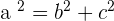
Eccentricity
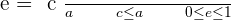
Horizontal major axis
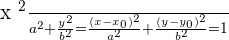
Vertical major axis
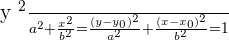
Hyperbola
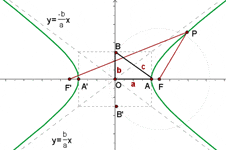
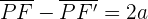
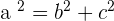
Eccentricity

Asymptotes
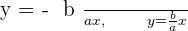
Horizontal transverse axis

Vertical transverse axis
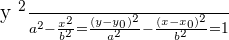
Rectangular hyperbola
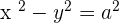
Asymptotes

Eccentricity
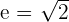
Equation determined by the asymptotes
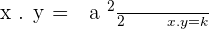
Parabola
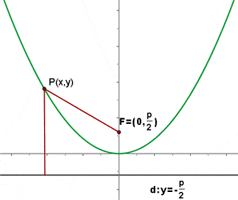
Parabolas with vertex at (0,0) and axis on the y-axis

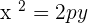
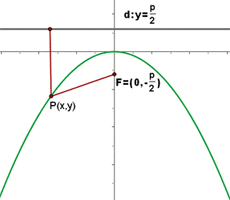
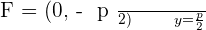
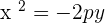
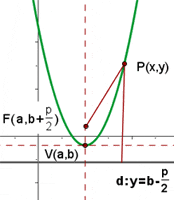
Parabola with vertex at (a,b) and axis parallel to the y-axis
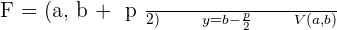

Parabola with vertex at (0,0) and axis on the x-axis
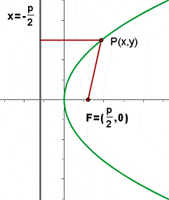
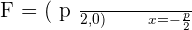


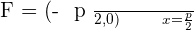
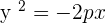
Parabola with vertex at (a,b) and axis parallel to the x-axis


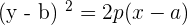
Summarise with AI:













