Chapters
There are many types of lines. These types help us to understand them properly. Horizontal and vertical lines are one of those types. In fact, they are very easy to understand and it doesn't require many concepts.

Horizontal Lines
If a line is parallel to the x-axis that means the line is a horizontal line. This type of line isn't influenced by the x-axis. In simple words, the x value doesn't matter in the case of the horizontal line, it will remain the same. The unique part of the horizontal line is that it passes through the y-intercept. That is why the equation of any horizontal line will be expressed in the terms of its y-intercept. Look at the below example for further clarification:

The y-intercept of the above graph is  , let's find the gradient of the above line.
, let's find the gradient of the above line.

In conclusion, no matter where the horizontal line is if it is a horizontal line, the slope of the line will always be equal to zero. Now, let's construct the equation of this line for point 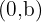 :
:

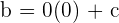

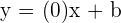
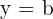
Hence, it is proved that the equation of the horizontal line will always be its y-intercept.
Example

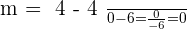
 for point
for point 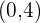
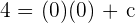


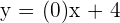

Vertical Lines
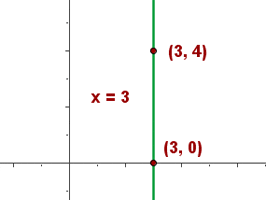
Like horizontal lines, vertical lines also exist. If the line is parallel to the ordinate, that means the line is a vertical line. When we talked about the horizontal line, the abscissa doesn't influence the line but, in the case of the vertical line, the abscissa influence the line but not the ordinate. In easy words, the vertical lines only depend on the x-axis but for any value of ordinate, the vertical line will remain the same. Last but not least, the vertical line passes through the x-axis which means it has an x-intercept. As a matter of fact, the whole equation depends on the x-intercept. Check the bottom example:

The x-intercept of the above graph is  , let's find the gradient of the above line.
, let's find the gradient of the above line.
 hence the answer will be infinity because any number divided by zero always result in infinity. In conclusion, the slope of a vertical line will always result in infinity. Now, let's construct the equation of this line for point
hence the answer will be infinity because any number divided by zero always result in infinity. In conclusion, the slope of a vertical line will always result in infinity. Now, let's construct the equation of this line for point 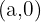 :
:
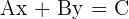
Since y component is zero:
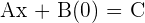
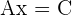
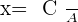
We can write 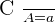 and
and  is the intercept hence we can conclude that the vertical lines depend on the x-intercept.
is the intercept hence we can conclude that the vertical lines depend on the x-intercept.
Example
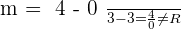

Axes Equations
The equation of the x-axis is y = 0 and the equation of the y-axis is x = 0.
Summarise with AI:













