Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10

Exercise 1
Find the symmetric point A', of the point  , with the line of symmetry:
, with the line of symmetry: 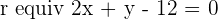 .
.
Exercise 2
Identify the type of triangle formed by the points: 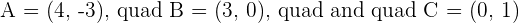 .
.
Exercise 3
Calculate the equation of the line that passes through the point 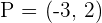 and is perpendicular to the line
and is perpendicular to the line 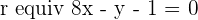 .
.
Exercise 4
The line 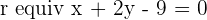 is the perpendicular bisector of the line segment AB whose endpoint A has the coordinates
is the perpendicular bisector of the line segment AB whose endpoint A has the coordinates  . Find the coordinates of the other endpoint.
. Find the coordinates of the other endpoint.
Exercise 5
Calculate the angle between the lines whose equations are:
1. 
2. 
Exercise 6
A straight line is parallel to the line 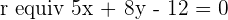 , and it is
, and it is  units from the origin. What is the equation of this line?
units from the origin. What is the equation of this line?
Exercise 7
Determine the equations of the angle bisectors formed by the lines:
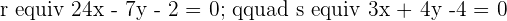
Exercise 8
The vertices of a parallelogram are 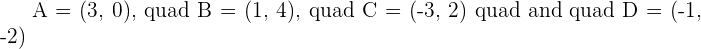 . Calculate the area.
. Calculate the area.
Exercise 9
Given the triangle formed by the points 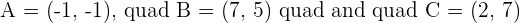 , calculate the equations of the heights and determine the orthocenter of the triangle.
, calculate the equations of the heights and determine the orthocenter of the triangle.
Exercise 10
A line is perpendicular to the line 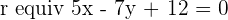 and it is
and it is  units away from the origin. Determine the equation of this line.
units away from the origin. Determine the equation of this line.
Solution of exercise 1
Find the symmetric point A', of the point  , with the line of symmetry:
, with the line of symmetry: 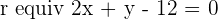 .
.

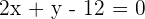
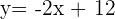
Comparing the above equation with 

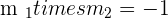
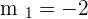
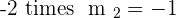


Using the co-ordinates of  to construct the line equation of
to construct the line equation of 

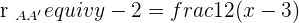
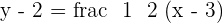
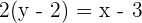
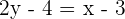
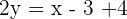
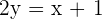
We have equations of both linear lines and now we will solve simultaneously to find the middle point:
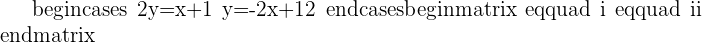
Multiplying equation ii by  :
:
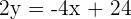 equation iii
equation iii
Since the unknown y is same in equation iii and equation i that means we can equate both sides of equation:
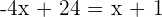


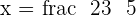
Substituting the value of x in the equation i:
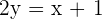
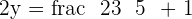

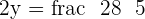

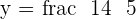
Hence the mid-point is M
Since M is the mid-point of AA' and we know the coordiantes of A that means we can calculate the coordinates of A' with the help of mid-point formula:
Mid point formula = 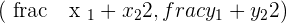
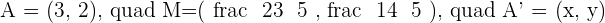
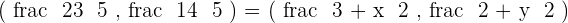
Equating each side of coordinates:


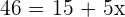
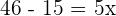
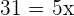
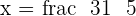

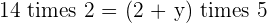




Hence, 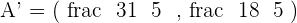
Solution of exercise 2
Identify the type of triangle formed by the points: 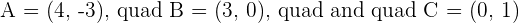 .
.

The distance of each side of the triangle will indicate the type of triangle. To calculate the distance, we will be using the distance formula.

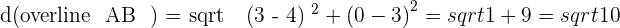
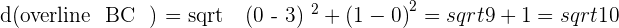
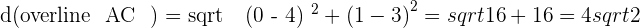
Since  , hence we can conclude that the triangle is an Isosceles.
, hence we can conclude that the triangle is an Isosceles.
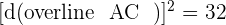
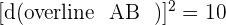
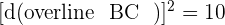
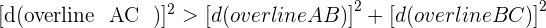 , hence we can conclude that the triangle is an obtuse triangle.
, hence we can conclude that the triangle is an obtuse triangle.
Solution of exercise 3
Calculate the equation of the line that passes through the point 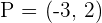 and is perpendicular to the line
and is perpendicular to the line 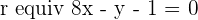 .
.
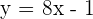

Comparing both equations to find gradient and y-intercept:

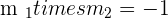

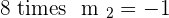
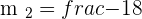
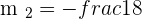

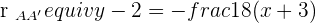
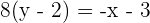
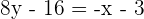
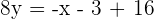

Solution of exercise 4
The line 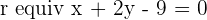 is the perpendicular bisector of the line segment AB whose endpoint A has the coordinates
is the perpendicular bisector of the line segment AB whose endpoint A has the coordinates  . Find the coordinates of the other endpoint.
. Find the coordinates of the other endpoint.

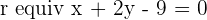
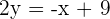
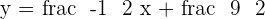

Comparing both equations:
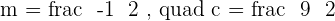
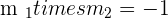

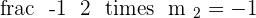
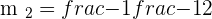
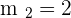

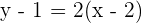
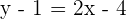



Solving both equations simultaneously will give us the cooridnates of mid-point because of the perpendicular bisector:



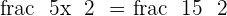
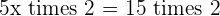
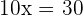
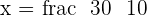

Substituting the value of x in the second equation:




Mid-point = 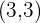 , A =
, A =  , B =
, B = 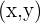
Mid point formula = 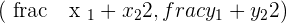
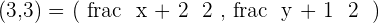
Equating each side of coordinates:


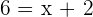
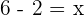

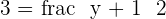

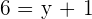
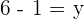

Hence the coordinates of B = 
Solution of exercise 5
Calculate the angle between the lines whose equations are:
1. 
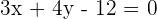
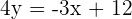
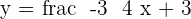

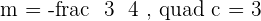
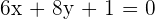
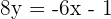

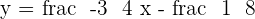
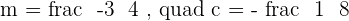


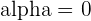
2. 

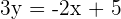
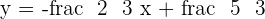


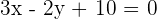
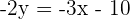


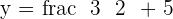

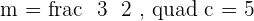
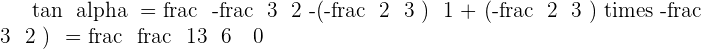
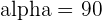
Solution of exercise 6
A straight line is parallel to the line 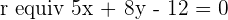 , and it is
, and it is  units from the origin. What is the equation of this line?
units from the origin. What is the equation of this line?
Since the line is parallel but deviated from the origin, the only difference between both lines will be the constant.
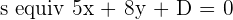
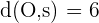
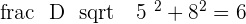
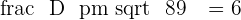


Solution of exercise 7
Determine the equations of the angle bisectors formed by the lines:
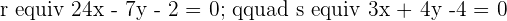
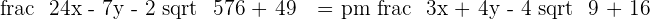
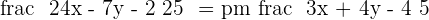
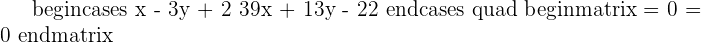
Solution of exercise 8
The vertices of a parallelogram are 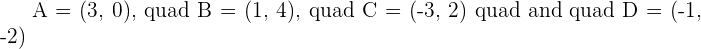 . Calculate the area.
. Calculate the area.
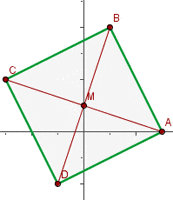
Area = 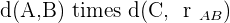
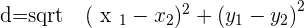
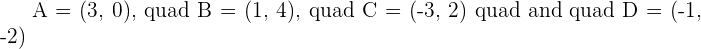

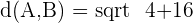

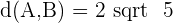
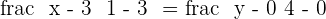
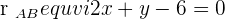

A = 
Solution of exercise 9
Given the triangle formed by the points 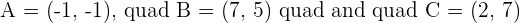 , calculate the equations of the heights and determine the orthocenter of the triangle.
, calculate the equations of the heights and determine the orthocenter of the triangle.

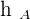 is perpendicular to
is perpendicular to 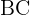
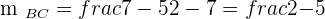
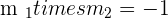
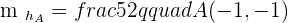
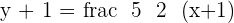

 is perpendicular to
is perpendicular to 

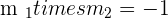

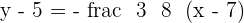
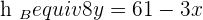
 is perpendicular to
is perpendicular to 
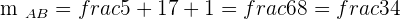
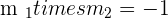
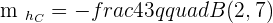


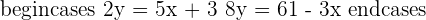
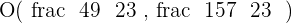
Solution of exercise 10
A line is perpendicular to the line 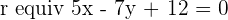 and it is
and it is  units away from the origin. Determine the equation of this line.
units away from the origin. Determine the equation of this line.
Since the line is perpendicular but deviated from the origin, the only difference between both lines will be the constant, and of course, the axis will switch.
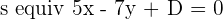

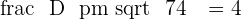
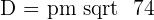
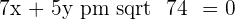
Summarise with AI:













