Chapters

What is a Line
A line in mathematics is one of the most important principles. Let’s take a look at the various equations for lines.

| Standard From | Slope-Intercept | Point-Slope Formula |
 |  |  |
When it comes to discussing perpendicular lines, the easiest formula to use is the slope-intercept formula, so that’s the one we’ll use. Keep in mind that you can write the equation of one line any of these three ways.
Let’s take a closer look at the slope-intercept formula. We have the following:
| (x,y) | The point | n/a |
| m | The slope | 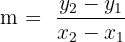 |
| b | The y-intercept, where the line touches the y axis | (0,y) |
What is an Angle
Angles are important concepts when talking about lines. In fact, an angle is formed by two lines. Take a look at the different angles below.
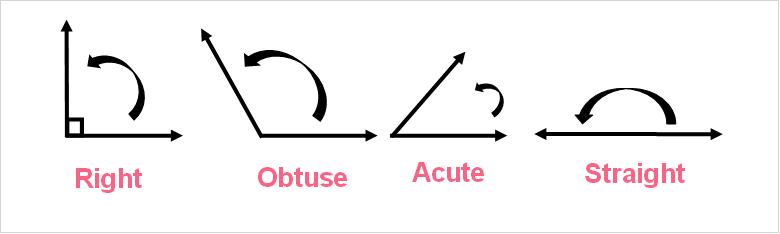
| Type | Degrees |
| Right | 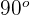 |
| Obtuse | 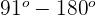 |
| Acute | 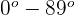 |
| Straight | 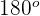 |
The most important angle when dealing with perpendicular lines is the right angle. Take note that the unit for angles is degrees. Here are the most common degrees.

| Degrees | Description |
| 90 | A corner |
| 180 | A straight line |
| 360 | A full circle |
What are Parallel Lines
There are two types of lines we generally talk about in maths: perpendicular lines and parallel lines. In order to fully understand what perpendicular lines are, you should know what parallel lines are.

Below are the properties of parallel lines.
| Property 1 | Never touch |
| Property 2 | Are always an equal distance apart |
| Property 3 | Can be parallel curves |
Let’s take a look at some examples of parallel lines. Can you tell which are parallel and which are not?

The corresponding answers are written below.
| A | B | C | D |
| Parallel | Curved parallel | Perpendicular | Not parallel |
Notice D in particular. Although the lines are not touching, they will at some point. We can tell this because if we kept drawing them further, they would eventually touch.
What are Perpendicular Lines
Now that you understand what lines are as well as what parallel lines are, let’s dive into perpendicular lines. Perpendicular lines are lines that form a right angle. Take a look at the definition below.
| Property 1 | Two lines that touch |
| Property 2 | Two lines form a right angle |
| Property 3 | Can be perpendicular planes |

That’s it! It’s that simple. However, it can be hard to spot what perpendicular lines are. Take a look below and try to tell which lines are perpendicular and which are not.
We won’t ever know which lines are perpendicular or not if we do not have the right angle marked in some way. You may have noticed already, but any time two lines form a right angle, they are marked with a square in the corner.

Perpendicular Lines Notation
When you have perpendicular lines, you can follow a certain notation. Let’s first take a look at two intersecting lines made up of four points.
| Line 1 | Line 2 | |
| Point 1 | A = (3, 5) | C = (2,1) |
| Point 2 | B = (3, -5) | D = (5, 1) |
When we look at these lines on a graph, we can see the lines between them. We can say that the lines they form correspond to the point they make.
| Line 1 | Made of point A and B | Line AB |  |
| Line 2 | Made of point C and D | Line CD |  |
When we have lines, we can actually write that line with the notation above, with a horizontal line above the name of the line or the name of the line made up of the two points that make it. When two lines are perpendicular, we can write it in the following notation.
| Line 1 | Line 2 | Perpendicular |
 |  | 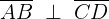 |
Slope Method
In order to tell whether two lines are perpendicular, you can try several different methods. The easiest method out of all of them is the slope method. Let’s take a look at how to use this method.
One of the properties of perpendicular lines is that their slopes be reciprocals. If you don’t know what a reciprocal is, let’s recap. Two numbers are reciprocals if they equal 1 when they are multiplied. Let’s take a look at an example:
\[
\frac{1}{3} \; * 3 = 1
\]
In order to find the reciprocal of a number, you usually only have to divide that number by 1. It’s easier to remember this rule:
| Example | Rule | Practice | |
| Fraction |  | Switch the denominator and numerator |  |
| Whole number | 4 | The fraction 1 over the whole number |  |
If you have a negative number, you have to make sure the reciprocal is also negative. This is because a negative times a negative is a positive.
When two lines have reciprocal slopes, they are perpendicular to each other.
Summarise with AI:













