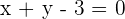Often we encounter equations like 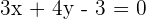 . These equations help us to understand the mechanism or any other object, however, constructing an equation of anything is also very important. For example, you have two points on a 2-D graph. You are asked to construct an equation of a line passing both points. Construction of an equation not only requires knowledge of general form but it also requires knowledge of the type of line, slope, and intercepts.
. These equations help us to understand the mechanism or any other object, however, constructing an equation of anything is also very important. For example, you have two points on a 2-D graph. You are asked to construct an equation of a line passing both points. Construction of an equation not only requires knowledge of general form but it also requires knowledge of the type of line, slope, and intercepts.

Equation of a Line
Whenever we talk about the equation of a line, there are three things that every line equation will have and they are x value, y value, and a constant. For example,  , in this equation you will find all three components but what about this line
, in this equation you will find all three components but what about this line 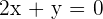 , you might be wondering there is no constant and a line equation should always have a constant. There is a constant but the value of that constant is zero which you can find on the right side of the equation. Here is another example
, you might be wondering there is no constant and a line equation should always have a constant. There is a constant but the value of that constant is zero which you can find on the right side of the equation. Here is another example 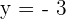 , take some time, and think about the x component. Let's rewrite this equation but in a different way,
, take some time, and think about the x component. Let's rewrite this equation but in a different way,  , if you multiply the zero with x, it will result in the example equation. Basically, the value of the x is zero and this can happen to y as well.
, if you multiply the zero with x, it will result in the example equation. Basically, the value of the x is zero and this can happen to y as well.
At this point, you must be wondering how equations are affected by making one component zero? Let's take a step back to our previous example (which was  ). We rewrote this equation
). We rewrote this equation  , what this means is the line isn't affected by increasing or decreasing the value of x. In simple words, the value of x doesn't play any role in this line, for example, we want to find the value of y when x is
, what this means is the line isn't affected by increasing or decreasing the value of x. In simple words, the value of x doesn't play any role in this line, for example, we want to find the value of y when x is  and the value of y is
and the value of y is  . For the same equation, let's find the value of y when x is
. For the same equation, let's find the value of y when x is  , the answer will be the same (i.e
, the answer will be the same (i.e  ). This means that any value of x, the value of y will remain constant. What if the constant value is zero? That is another case.
). This means that any value of x, the value of y will remain constant. What if the constant value is zero? That is another case.
The constant in an equation is basically y-intercept. In easy words, the y-intercept is the point at which the line cuts the y-axis. For example, here is an equation of a line,  . Let's rearrange it in form of
. Let's rearrange it in form of  ,
, 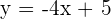 , the
, the  is the y-intercept. It means that the line intersects the y-axis at
is the y-intercept. It means that the line intersects the y-axis at  . If the y-intercept is equal to zero, that means the line passes through the origin (which is
. If the y-intercept is equal to zero, that means the line passes through the origin (which is  ).
).
What if the x, as well as y components, become zero? Then the result would not be an equation. That is why both components cannot be zero at the same time. In mathematical language, we express it as 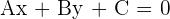 , A, B, and C are constants, and the values of A and B cannot both be equal to zero. The equation is usually written with a positive value for A. You can find the slope of the line by
, A, B, and C are constants, and the values of A and B cannot both be equal to zero. The equation is usually written with a positive value for A. You can find the slope of the line by  . The direction vector is:
. The direction vector is: 
How to Construct the Equation of a Line Through Given Points?
To find the equation of a line, we use this formula  . However, in many textbooks, you might see an alternative formula which is
. However, in many textbooks, you might see an alternative formula which is  . You can use any formula you want. Both formulas has their pros and cons. Using
. You can use any formula you want. Both formulas has their pros and cons. Using  formula will consume more time than using
formula will consume more time than using  formula. On the other hand, you can only use
formula. On the other hand, you can only use  to find gradient and y-intercept of any linear line you want, you can't do this with
to find gradient and y-intercept of any linear line you want, you can't do this with  formula.
formula.  formula is a derived formula and below is its derivation:
formula is a derived formula and below is its derivation:
Consider two points 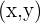 &
& 


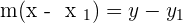

Finding the equation of a line is very easy. To make it easier, we came up with some steps for finding the equation of a line. Before we start, don't forget that whatever we have told you is about linear lines, for other lines (such as quadratic lines, polynomial lines, etc.) everything is different. Below are the steps for finding the equation of a linear line.
Q. Find the equation of a line that passes through points A = 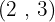 and B =
and B = 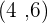 .
.
Step 1: Find the Gradient/Slope

A = 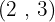 and B =
and B = 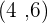 .
.


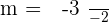
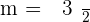
Step 2:
Use any equation formulas to find the equation of the given points. We are using  . In addition, you need to select one of the provided points, we are selecting B =
. In addition, you need to select one of the provided points, we are selecting B = 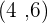 . You will get same answer if you use
. You will get same answer if you use  formula or A =
formula or A = 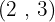 or both.
or both.
Step 3:
Once you made your decision, execute it.

B = 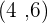
Place the values of x and y in 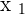 &
&  :
:
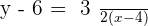


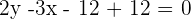
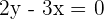
Examples
Determine the equation in general form of the line that passes through Point 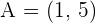 and has a slope of
and has a slope of 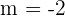 .
.
Using  to find the equation:
to find the equation:

Substituting the value of x, y, and m in the above equation to find the value of y-intercept:

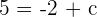

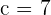
Reuse the formula once again to find the final equation of the line but this time, substitute the value of y-intercept and slope only:

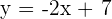

Write the equation in the general form of the line that passes through points A =  and B =
and B = 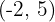 .
.

A =  and B =
and B = 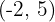 .
.
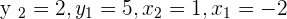

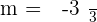
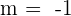
Using  to find the equation of the line. We will substitute the value of x, y, and m to find the value of y-intercept. Considering point A =
to find the equation of the line. We will substitute the value of x, y, and m to find the value of y-intercept. Considering point A = 
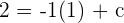
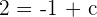

Reuse the formula once again to find the final equation of the line but this time, substitute the value of y-intercept and slope only: