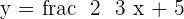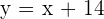Slope-Intercept Form
Every line and curve has an equation that defines its behavior. The question is what information can we extract from the equation? The easiest answer is the slope and intercept. Finding slope and intercept of the curve is very complex, let's just stick to straight lines only. Let's take a look at some linear equations below:
Did you notice something similar? All the above equations follow some kind of linear pattern, a syntax maybe? If you thought about that then here is another piece of information for you, yes they do follow a syntax. Hence, it is safe to say that linear equations are usually in this form:

Here, x and y represent the axes of the graph but what about the variables m and b? The value "m" represents the gradient/slope of the line. On the other hand, the value "b" represents the y-intercept. The best part is that you can use this syntax to find the slope and y-intercept of any linear equation. All you need to do is to compare the provided linear equation with this syntax. Here is an example, consider the first example of the linear equations, i.e. 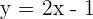 . To find the slope and intercept, you need to compare it with the syntax like this:
. To find the slope and intercept, you need to compare it with the syntax like this:
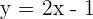

If we compare both equations, we found that the value of m is equal to  and the value of b is equal to
and the value of b is equal to  . Therefore, the slope of the first example is
. Therefore, the slope of the first example is  and the y-intercept is
and the y-intercept is  . Here is an advice, the y coordinate has a constant of
. Here is an advice, the y coordinate has a constant of  . In easy words, always keep the constant of y coordinate equal to
. In easy words, always keep the constant of y coordinate equal to  . Consider the last example of linear equations, i.e.
. Consider the last example of linear equations, i.e. 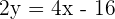 . The constant of y is
. The constant of y is  in this example, to make it
in this example, to make it  we need to divide the right-hand side with
we need to divide the right-hand side with  .
.
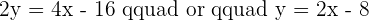
Use the equation, 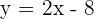 to find the value of slope and y-intercept.
to find the value of slope and y-intercept.
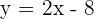

The slope of this equation is  and the y-intercept is
and the y-intercept is  . Why don't you find the slope and intercept of the rest linear equation examples and let us know in the comment section what you found?
. Why don't you find the slope and intercept of the rest linear equation examples and let us know in the comment section what you found?
Using Slope and Intercept to Form Equation
You don't have the equation but you do know any single point and the slope of the line then there is nothing to worry about. You can form the equation using the same syntax, which is  . The first step is to find the y-intercept. To calculate the intercept, you need to input the slope and point coordinates in their respective places. This way you will calculate the value of the intercept. The second and last step is to write the syntax and then insert the value of slope and intercept in their respective places and that is how you form an equation of a line using slope and coordinates of a point.
. The first step is to find the y-intercept. To calculate the intercept, you need to input the slope and point coordinates in their respective places. This way you will calculate the value of the intercept. The second and last step is to write the syntax and then insert the value of slope and intercept in their respective places and that is how you form an equation of a line using slope and coordinates of a point.
Example
Calculate the equation (in slope–intercept form) of the line that passes through Point 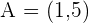 and has a slope
and has a slope 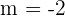 .
.

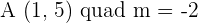
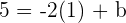
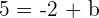
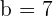

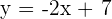
Summarise with AI: