Chapters

Distance Formula
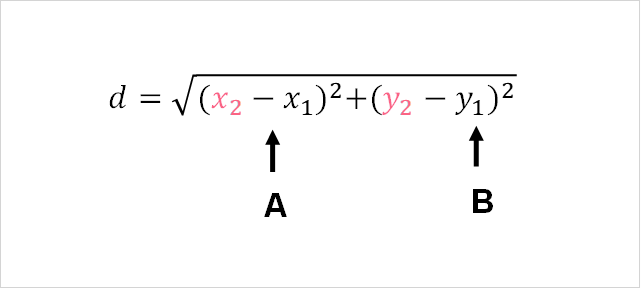
The variables in this formula correspond to the coordinates of the two points you’re trying to find the distance between.
| A | X coordinates of both points |
| B | Y coordinates of both points |
In order to understand when two lines intersect, you should be able to find the distance between any two points. If you’re unfamiliar with coordinates, coordinates are simply a set of numbers that tell you where a point is on a plane.
Take a look at some examples below.
| x | y |
| 2 | 5 |
| 1 | 4 |
| 3 | 8 |
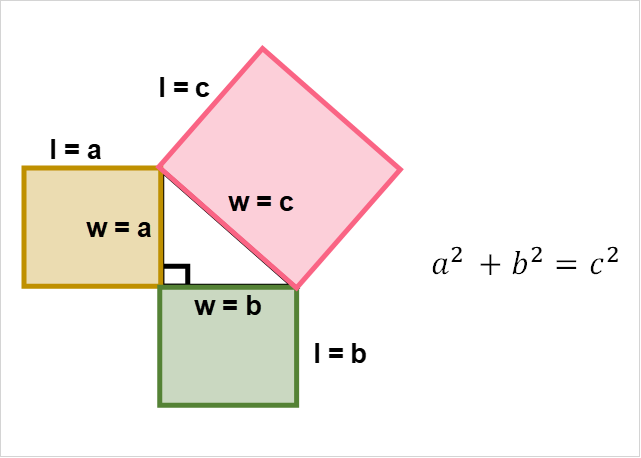
Pythagorean Theorem
The distance formula comes from the Pythagorean theorem. The Pythagorean theorem deals with right triangles and states the following.
| Definition | Situation | Equation | |
| Pythagorean Theorem | When you have a right triangle, you can find the length of any side if you know the length of the other two sides | Right triangles | 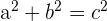 |
Parallel Lines
In geometry, we’re usually dealing with two different types of lines: intersecting and parallel lines. Before we get into intersecting lines, let’s make sure we know what parallel lines are. Take a look at the definition below.
| Requirement 1 | Requirement 2 | |
| Lines are parallel if they: | Are always at the same distance from each other | Never touch each other |
Let’s take a look at some examples of parallel lines.

| A | B | C |
| Parallel | Parallel | Not parallel |
If you want to test whether two lines are truly parallel, you can draw an intersecting line and check the angles this intersecting line makes. If the corresponding angles are the same, that’s one way to check that the lines are parallel.
Intersection Definition
Okay, now let’s talk about the other type of lines: intersecting lines! When two lines intersect, it simply means that they touch each other at one point. Take a look at the definition below.
| Requirement 1 | Requirement 2 | |
| Lines are intersecting if they: | Are not parallel | Touch each other one time at most |
It’s a pretty simple concept, but let's take a look at some examples below.

| A | B | C |
| Not intersecting | Intersecting | Intersecting |
You might be wondering why C is considered as intersecting. After all, they don’t touch each other at one point. Well, even though they aren’t touching each other in the image shown, they do touch each other at one point if you were to continue drawing them out.
Equation of a Line
In order to find out whether two lines are intersecting, you should fully understand what the equation of a line is. Take a look at the two forms you’re likely to encounter below.
| General Form | Point-Slope Form |
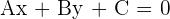 |  |
Both of these equations will give you the equation of any line. The only difference is that in some cases it’s easier to use one than the other. In this case, we’ll use the general form.
Equation of Two Lines
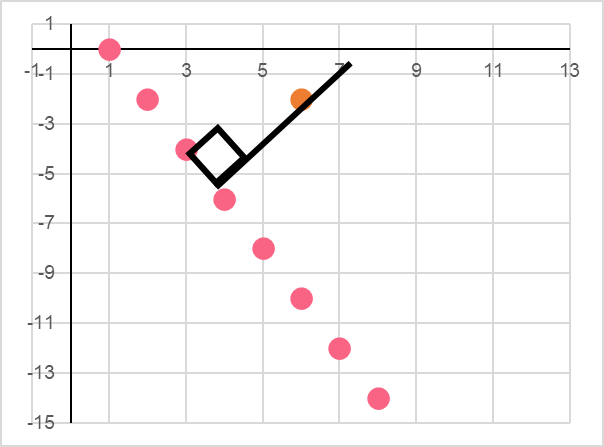
Let’s say that you’re given a point and a line. How can you find the point of intersection where the point and the line would meet? Take a look at the image below.

| Equation of the line | y=-2x+2 |
| Point | (6,-2) |
Here, the equation for the line as well as the coordinates of the point are given.
The way we would solve this is to try to find the point of intersection, which is where the line that the point is on crosses the line.
When a line is perpendicular to another line, the angle those two lines form is a right angle. In other words, perpendicular lines are lines that intersect at 90 degrees.
This would be the shortest distance between any point and a line is with the line that forms a perpendicular intersection with the line. So this is the point of intersection we will find.
The first step is to find the equation of the line that contains the point. Follow the steps below.
| Step 1 | Perpendicular lines have slopes that are reciprocal to each other. | Slope of line: -2 Reciprocal: |
| Step 2 | Plug the slope and the point into the line equation to find b, the y-intercept. | -2 =  (6) + b (6) + b |
| Step 3 | Simplify | -2 = 3 + b |
| Step 4 | Solve for b | b = -2 - 3 = -5 |
| Step 5 | Equation of the line | y= x -5 x -5 |
Now, we have the equation of the line that contains the point (6, -2).
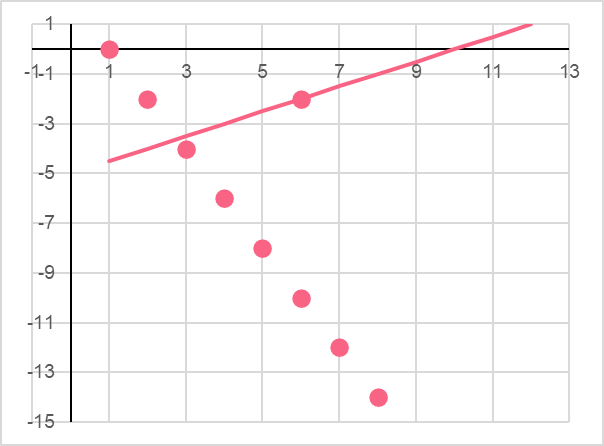
Solving for the Point of Intersection
Now that we have the two lines, we can solve for the point of intersection. Recall that the point of intersection is the point where the two lines intersect. In this case, the intersecting lines are a special type of intersecting lines: perpendicular lines.
The point at which two lines meet is where the two lines equal each other. This is pretty obvious: no matter what the equation of the lines, the point where the two lines touch is one point which they share.

So, at this point, the x and y value of the two lines are the same: at that point they share one coordinate (x,y).
So we simply have to set the equations of each line equal to one another. Follow the steps below.
| Step 1 | Equation of two intersecting lines | y = -2x + 2 y= |
| Step 2 | Set the equations equal to one another | 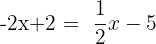 |
| Step 3 | Move the x values to one side | 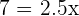 |
| Step 4 | Solve for x | x=2.8 |
Now that we have the x value, we simply need to plug it back into the equation.
| Step 1 | Get any of the equations of the two lines | y=-2x+2 |
| Step 2 | Plug in the x value | y=-2(2.8)+2 |
| Step 3 | Solve for y | y=7.6 |
So, the point of intersection is (2.8, 7.6).
Summarise with AI:













