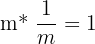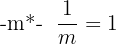Chapters

Mathematical Plane
Before we dive into what a slope is, it’s important to understand what a plane is in mathematics. When we talk about planes, we are usually referring to a Cartesian plane. Check one out below.
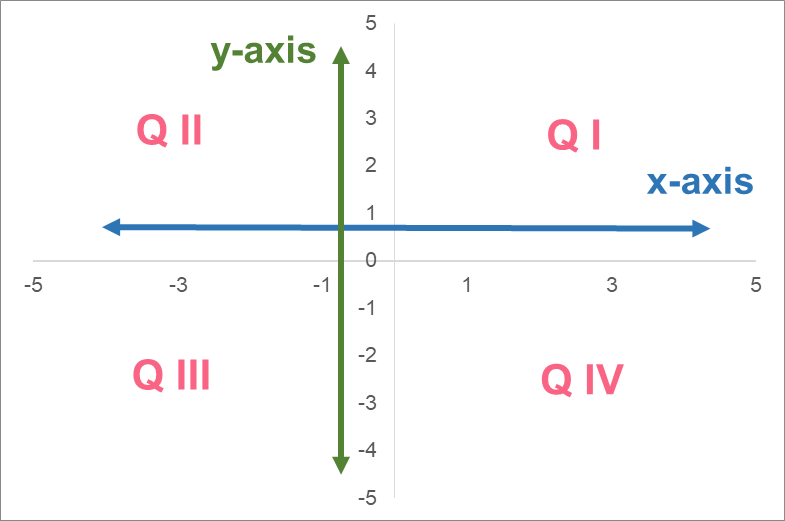
There are a couple of characteristics that all graphs have. Let’s take a look at some of those characteristics below.
| Characteristic | Description |
| 1 | Four quadrants. These quadrants go counter-clockwise. |
| 2 | Two axes: an x axis and a y axis. |
| 3 | There are only four directions you can go in: up or down, left or right. |
Distance Between Two Points Formula
It is important to know the formula you use to find the distance between two points. First, you should understand what points are on a graph.
| Formal Name | Definition | Standard Form | Explanation | Example | |
| Point | Coordinates | Coordinates that give you directions to how to get to a point on a graph | (x,y) | (x-coordinate, y-coordinate) | (-5, -2) |
As you can see from the definition above, you can have almost any combination of points as long as they give you at least an x-coordinate and a y-coordinate.
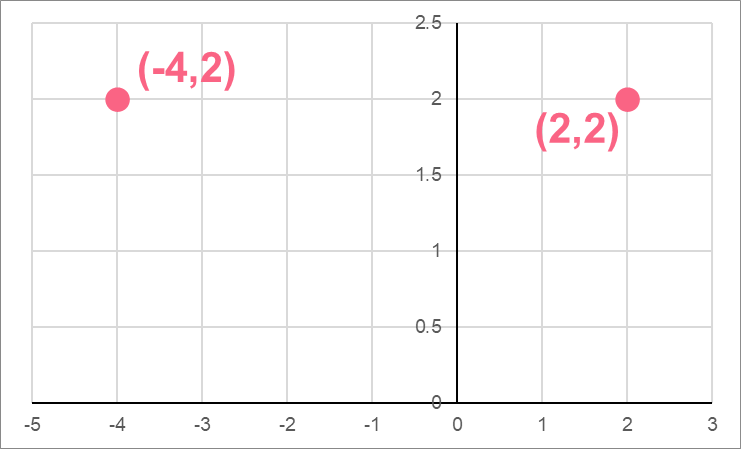
| x-coordinate | y-coordinate | |
| A | -4 | 2 |
| B | 2 | 2 |
To find the distance between these two points, you simply have to follow the distance formula.
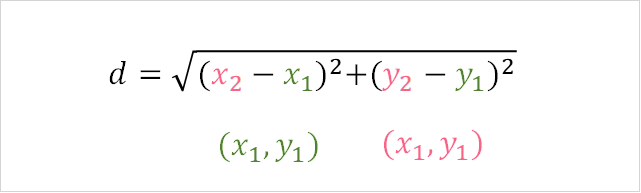
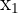 | 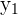 |  |  |
| -4 | 2 | 2 | 2 |
Equation of a Line
Now, let’s introduce the concept of a slope. The term slope in maths is similar to what you encounter in real life: like the slope of a hill. The only difference is that in maths we’re referring to lines. Let’s take a look at the standard equation of a line.

This is called the slope-intercept formula because it includes the y-intercept (b) and a slope.
| The point | (x,y) |
| Slope | m |
| Y-intercept | b |
Slope Formula
The slope can be thought of as the incline or decline of the line. You can think of the slope of a line as the amount you rise over the amount you run.
In reality, we can go in two directions.
| Positive Direction | Negative Direction | |
| y-axis | Rise (Up) | Down |
| x-axis | Run (Right) | Left |
Slope Formula Given Two Points
To have a slope, you need to have at least two points. This is because any two points form a line. If you just have one point, you can’t really have a slope because there are infinitely many directions you can go from that point.
To find the slope between two points, you should follow the slope formula.
| m |  |  | 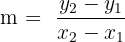 |
| slope | Point 1 | Point 2 | Slope formula |
Slope Formula of Parallel Lines
Parallel lines are one of the two special types of lines. In order to have parallel lines, you have to satisfy the following conditions.

| A | Condition 1 | Lines are equal distance to each other always |
| B | Condition 2 | Lines don’t ever touch, no matter how long they go for |
Finding the slope between two parallel lines is the easiest to find. Check out the rules below.
| Two lines are parallel | The slopes of the two lines are equal | y=(m)x+b y=(j)x+b | m=j |
Slope Formula of Perpendicular Lines
Perpendicular lines are the second type of line. When two lines touch, they are said to intersect. This is easy enough to remember - just think of a street intersection. A street intersection is where two streets meet each other.
| Condition 1 | Perpendicular lines are intersecting |
| Condition 2 | They have a point of intersection |
| Condition 3 | Their lines form a right angle (90 degrees) |
Perpendicular lines are a special type of intersecting lines. Finding the slope between two perpendicular lines is a bit harder.
| Two lines are perpendicular | The slopes of the two lines are reciprocals | y=(m)x+b y=(j)x+b | (j)=reciprocal of (m) |
In order to find the reciprocal, you should take a look at the table below.
| Definition | |
| Reciprocal | When a number (m) and it’s reciprocal (j) are multiplied together, they equal 1. |
| Reciprocal of positive number | Reciprocal of m = 
|
| Reciprocal of negative number | Reciprocal of -m = 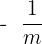
|
Example 1
Let’s go through a step-by-step example of how to find the slope of the following two points.
| Point 1 | (3, 6) |
| Point 2 | (-2, 8) |
In order to find the slope of two points, we must use the formula of the slope between two points. Recall that this is simply the two y coordinates subtracted from each other divided by the two x coordinates subtracted by one another.
\[
m = \dfrac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{8-6}{-2-3} = \dfrac{2}{-5}
\]
The slope between these two points is 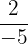 .
.
Example 2
Using what you know about parallel lines, give an equation of a line that is parallel to the following line.
\[
y=-3x+10
\]
In order to solve this, we simply need to remember that parallel lines have the same slope. Therefore, we can make any combination of lines.
| 1 | y=-3x |
| 2 | y=-3x+1 |
| 3 | y=-3x-15 |
Example 3
Find the slope of any line perpendicular to the following line.
\[
y= -\dfrac{1}{3}x + 1
\]
We simply need to find the reciprocal.
| The slope | Divide 1 by the slope | Check |
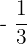 | 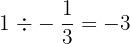 | 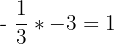 |
Any line we make with a slope of -3 will be perpendicular to this line.
Summarise with AI: