Exercise 1
Write the equation (in all possible forms) of the line that passes through the points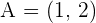
and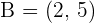
.
Exercise 2
Identify the type of triangle formed by the points: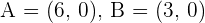
and
.
Exercise 3
Determine the slope and y-intercept of the line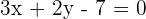
.
Exercise 4
Find the equation of the line r which passes through the point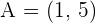
and is parallel to the line
.
Exercise 5
Find the equation of the line that passes through the point
and is parallel to the straight line that joins the points
and
.
Exercise 6
The points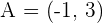
and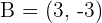
are vertices of an isosceles triangle ABC that has its apex C on the line
. If AC and BC are the equal sides, calculate the coordinates of Point C.
Exercise 7
The line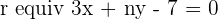
passes through the point
and is parallel to the line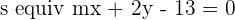
. Calculate the values of m and n.
Exercise 8
Given triangle ABC with coordinates
and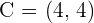
, calculate the equation of the median that passes through the vertex C.
Exercise 9
A parallelogram has a vertex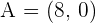
, and the point of intersection of its two diagonals is
. If the other vertex is at the origin, calculate:
1 The other two vertices.
2 The equations of the diagonals.
3 The length of the diagonal.
Solution of exercise 1
Write the equation (in all possible forms) of the line that passes through the points 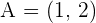and .
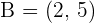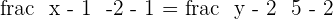
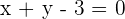
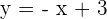
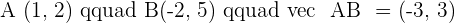
Solution of exercise 2
Identify the type of triangle formed by the points: 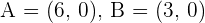and .
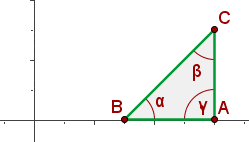
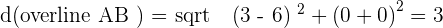
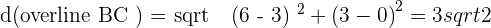
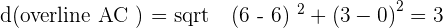
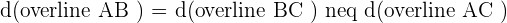Isosceles
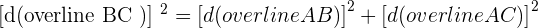Right triangle
Solution of exercise 3
Determine the slope and y-intercept of the line .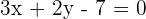
Solution of exercise 4
Find the equation of the line r which passes through the point 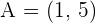and is parallel to the line .
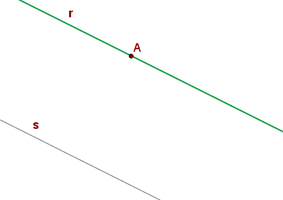
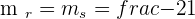
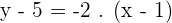
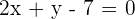
Solution of exercise 5
Find the equation of the line that passes through the point and is parallel to the straight line that joins the points and .
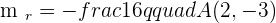
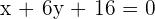
Solution of exercise 6
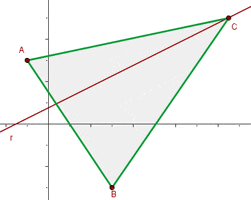
The points 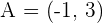and 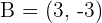are vertices of an isosceles triangle ABC that has its apex C on the line . If AC and BC are the equal sides, calculate the coordinates of Point C.
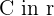
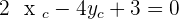
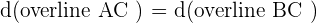
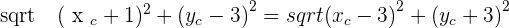
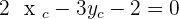
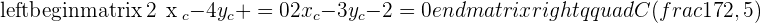
Solution of exercise 7
The line 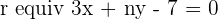passes through the point and is parallel to the line 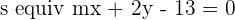. Calculate the values of m and n.
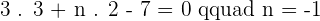
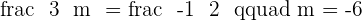
Solution of exercise 8
Given triangle ABC with coordinates and 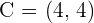, calculate the equation of the median that passes through the vertex C.
Solution of exercise 9
A parallelogram has a vertex 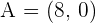, and the point of intersection of its two diagonals is . If the other vertex is at the origin, calculate:
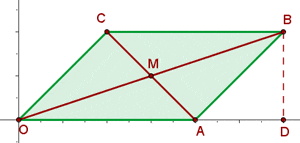
1 The other two vertices.
M is the midpoint of
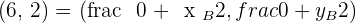
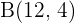
M is the midpoint of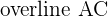
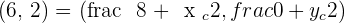
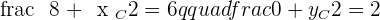
2 The equations of the diagonals.
Equation of AC
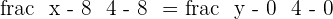
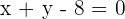
Equation of OB
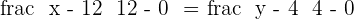
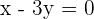
3 The length of the diagonal.
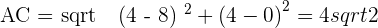
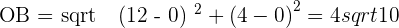
Summarise with AI:
Did you like this article? Rate it!
Loading...
