Chapters

What is a Plane?

| Quadrant | X-axis | Y-axis | Coordinates | |
| A | I | Positive | Positive | (+,+) |
| B | II | Negative | Positive | (-,+) |
| C | III | Negative | Negative | (-,-) |
| D | IV | Positive | Negative | (+,+) |
Point Definition
A point on a plane is defined by coordinates. You can think of coordinates as a set of directions to arrive to a point on a plane.
| Definition | Standard Form | Example | |
| Coordinates | A set of numbers that help you place a point on a plane | (x coordinate, y coordinate) | (2,-5) |
Let’s take a look at an example.
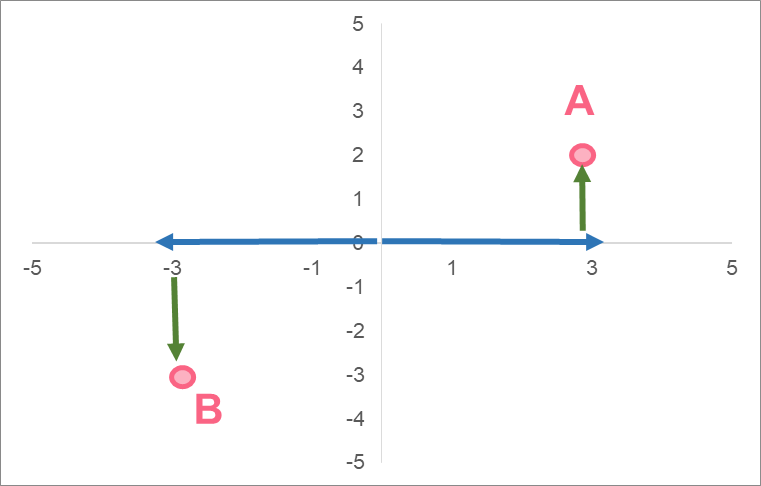
If we didn’t have a standard form for coordinates, we could say the following:
| Directions | |
| A | Move 5 places to the right, go up 2 spaces |
| B | Move 3 spaces to the left, go 1 space down |
Instead of having to give these directions all the time, we can just give the coordinates of a point. Keep in mind that both the x and y coordinates only move in two directions:
| Coordinate | Possible Directions | Positive Direction | Negative Direction |
| x | Left or Right | Right | Left |
| y | Up or Down | Up | Down |
Formula Distance Between Two Points
When you want to find the distance between two points, you simply follow the formula below.
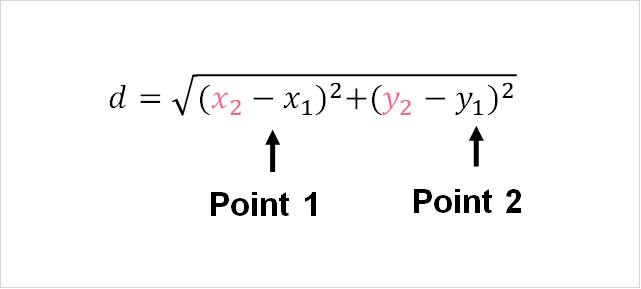
Here, you can see what the formula means.
| Coordinates | X | Y | |
| Point 1 |  | 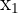 | 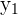 |
| Point 2 | 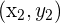 |  |  |
Example 1
Let’s go through an example together. Take the following two points.
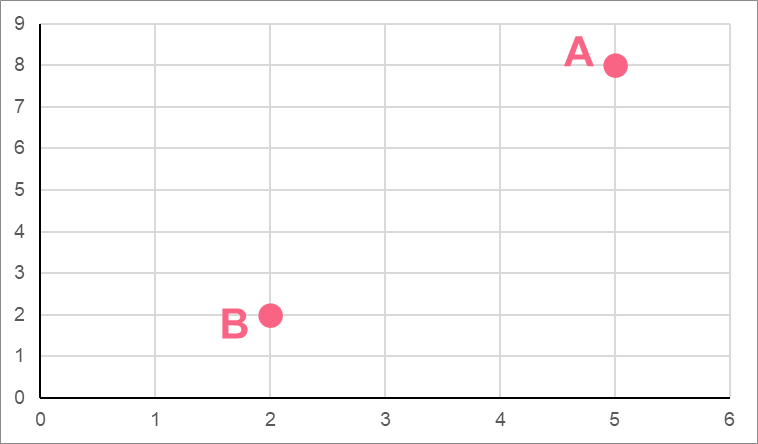
| Standard Forms | Coordinates | |
| Point A |  | (2,2) |
| Point B | 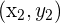 | (5,8) |
To make it easier, let’s split up the coordinates like we did in the previous section. This way, we can simply plug it into our formula.
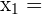 | 2 |
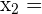 | 5 |
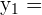 | 2 |
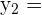 | 8 |
In order to find the distance, we simply need to plug it into the distance formula.

| Step 1 | Plug in the coordinates |  |
| Step 2 | Simplify the equation | 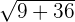 |
| Step 3 | Take the square root |  |
Pythagorean Theorem
You may be wondering if there’s an easier way to find the distance between two points. Another way to find the distance between two points is if you have a right triangle on the graph.
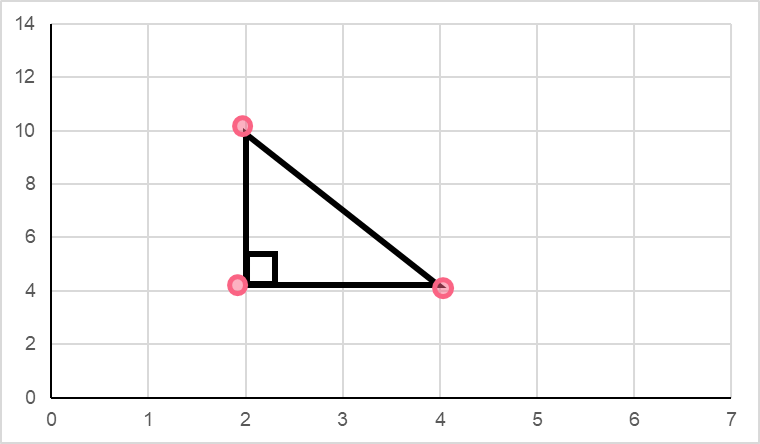
In this case, you can use the Pythagorean theorem. Take a look at the information below.
| Right triangle | To use the Pythagorean theorem, you must have a right triangle, which is a triangle whose largest angle is 90 degrees. |
| Two sides | You must know the length of at least two sides in order to find the length of the last side. |
| Hypotenuse | The hypotenuse (c) is the largest side in a right triangle. The hypotenuse is always the side that is opposite the right angle. |
In this case, you can use the Pythagorean theorem as long as you have the length of two sides.

| Pythagorean Theorem | 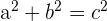 |
Problem 1
Find the distance between the origin of the graph and the point given below.
| Coordinates | |
| Point A | (4,5) |
Problem 2
On a graph, you have a square made up of four points. You know two of those points - find the length of the diagonal. Next, find area of the triangle formed by the square’s diagonal.
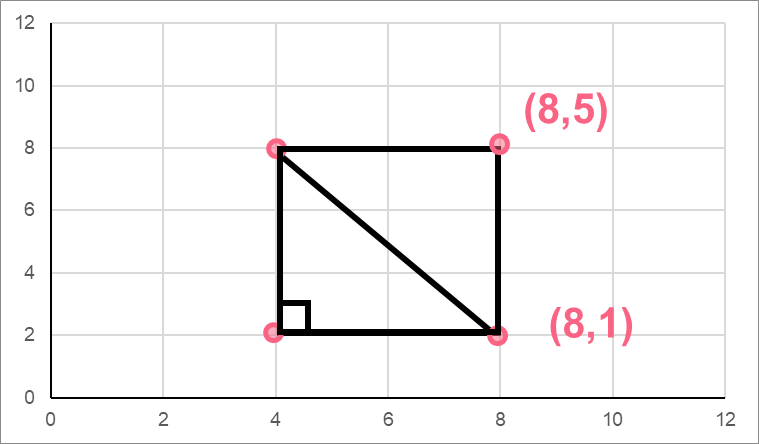
| Point 1 | (8,5) |
| Point 2 | (8,1) |
Solution Problem 1
In order to find the distance from the origin to the point, you should know what the origin is. Recall that the origin is located in the middle of the graph.
| Coordinates | |
| Origin | (0,0) |
| Point A | (4,5) |
So, to find the distance from the point given to the graph, we simply need to plug the two points into the distance formula.
| Step 1 | Get the distance formula | 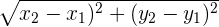 |
| Step 2 | Plug in the points | 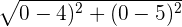 |
| Step 3 | Solve the equation |  = 6.4 = 6.4 |
The length between the origin and the point is 6.4.
Solution Problem 2
In this problem, we need to find the area of the square. However, we only have the coordinates of one side. To solve the problem, you should recall a couple of facts.
| Fact 1 | All the sides of a square have the same length |
| Fact 2 | A square is made up of four right angles |
| Fact 3 | Because of these right angles, the diagonal of a square makes a hypotenuse |
So, the first step is to find the distance between the two points we’re given: (8,1) and (8,5).
| Step 1 | Get the distance formula | 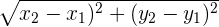 |
| Step 2 | Plug in the points | 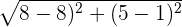 |
| Step 3 | Solve the equation |  = 4 = 4 |
Because all sides of a square are the same length, we know that a = b.
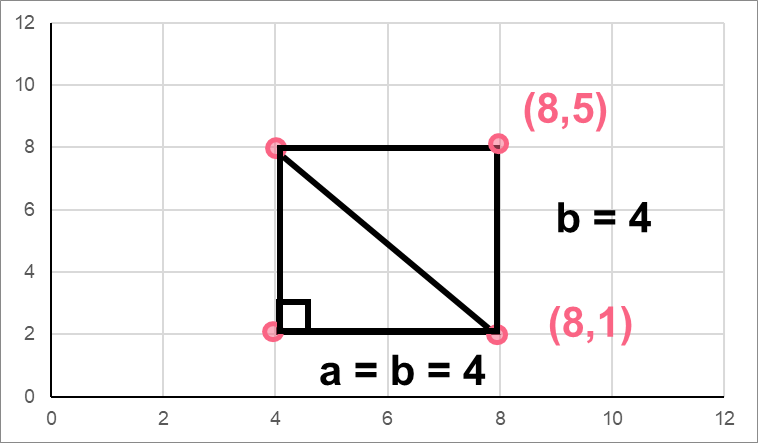
Recall the formula for the area of a triangle.
| Step 1 | Formula for the area of a triangle | 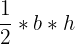 |
| Step 2 | Plug in the base (b) and the height (h) of the triangle | 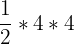 |
| Step 3 | Solve the equation | 8 |
The area of the triangle is 8.
Finally, because we’re dealing with a right triangle, we can simply use the Pythagorean to discover the length of the diagonal.
| Step 1 | Get the Pythagorean formula | 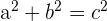 |
| Step 2 | Plug in the points |  |
| Step 3 | Solve the equation | 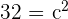 |
| Step 4 | Take the square root | 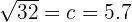 |
Summarise with AI:













