
What is an Intercept and How to Find Intercepts?
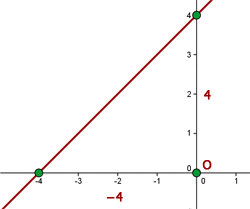
Intercepts are the point at which the graph intersects the axes. Usually, we work in 2-dimension which means that there are two axes: the x-axis (abscissa) and y-axis (ordinate). Since intercepts are related to axes, there are two types of intercepts: x-intercept and y-intercept. If the graph crosses the x-axis, the graph's point intersects the x-axis is the x-intercept. If the graph intersects the y-axis, the graph's point intersects the y-axis is called the y-intercept. For better understanding, check the below graph:
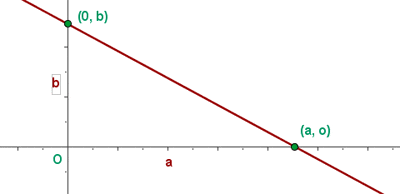
The graph intersects both axes but which one is the x-intercept and which one is the y-intercept. The point,  is the x-intercept and the point
is the x-intercept and the point  is the y-intercept. Did you notice something? The coordinates of the intercepts have their opposite axis equal to zero. Consider the x-intercept,
is the y-intercept. Did you notice something? The coordinates of the intercepts have their opposite axis equal to zero. Consider the x-intercept,  , the y-axis is zero and the same thing is happening in the y-intercept as well. Is this an incident? No, the opposite axis should always be zero when finding the intercept. In simple words, the y-axis in the x-intercept should always be zero and the x-axis in the y-intercept should always be zero.
, the y-axis is zero and the same thing is happening in the y-intercept as well. Is this an incident? No, the opposite axis should always be zero when finding the intercept. In simple words, the y-axis in the x-intercept should always be zero and the x-axis in the y-intercept should always be zero.
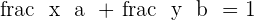
a is the x-intercept.
b is the y-intercept.
a and b must be nonzero.
The values of a and b can be obtained from the general form equation.
If 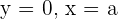 .
.
If  .
.
Imagine you are given an equation of a line, 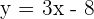 , and your teacher asks you to find the x-intercept as well as the y-intercept. The solution is pretty simple, we will find the x-intercept first, but it is your choice which intercept you want to find first. For the x-intercept, we know that the y-axis will be equal to zero. Apply this condition to the equation:
, and your teacher asks you to find the x-intercept as well as the y-intercept. The solution is pretty simple, we will find the x-intercept first, but it is your choice which intercept you want to find first. For the x-intercept, we know that the y-axis will be equal to zero. Apply this condition to the equation:
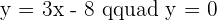
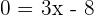
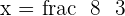
Many students make this common mistake. They finish till here but there is one thing they are missing. The question asked for the x-intercept's coordinate, therefore, end the answer with the coordinates of the respective intercept. Since we were finding the x-intercept, the final answer will be  , now let's find the y-intercept.
, now let's find the y-intercept.
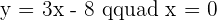
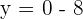
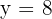
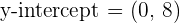
Some Important Points to Note
A line does not have an intercept form equation in the following cases:
1.A line parallel to the x-axis, which has the equation 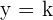 .
.
2.A line parallel to the x-axis, which has the equation 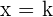 .
.
3.A line that passes through the origin, which has equation  .
.
Examples
Example 1
A line has an x-intercept of  and a y-intercept of
and a y-intercept of  . Find its equation.
. Find its equation.
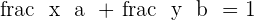
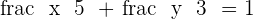
Example 2
The line 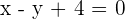 forms a triangle with the axes. Determine the area of the triangle.
forms a triangle with the axes. Determine the area of the triangle.
The line forms a right triangle with the origin and its legs are the axes.
If 
If 
The intercept form is:
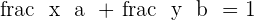

The area is:
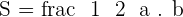
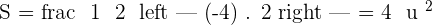
Example 3
A line passes through the point 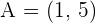 and creates a triangle of
and creates a triangle of 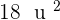 with the axes. Determine the equation of the line.
with the axes. Determine the equation of the line.
Apply the intercept form:
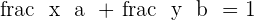

The area of the triangle is:
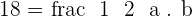
Solve the system:

After solving simultaneously, the results are:
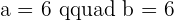
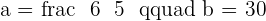
Therefore,
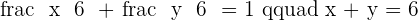
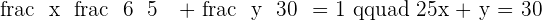
Example 4
A line forms a triangle with the axes where the length of the leg formed by the x-axis is twice the length of the leg formed by the y-axis. If the line passes through the point  , what is its equation?
, what is its equation?

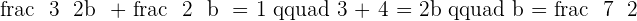
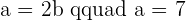
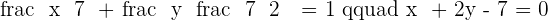
Summarise with AI:













